
���� ��1���ٹ�E��EH��x����H����֤����AOD�ա�DHE�������DH��EH��DO���ɱ�ʾ��E�����ꣻ�ڰ�E�������������ֱ�߽���ʽ������֤�ý��ۣ�
��2����E��EH��x����H����֤����AOD�ס�DHE���������������ε����ʿ����DH��EH���ɵó�E�����꣬��ɵó���E���ֱ�ߵĽ���ʽ��
��3����������ɽ�Rt��AOB����������λ����Rt��CFG���ѣ�2����ֱ������ƽ��������λ���ɵõ�����������ֱ�ߣ�
��� �⣺��1���ٹ�E��EH��x����H����ͼ1��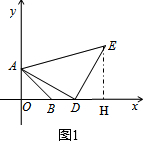
�ڵ���Rt��ADE�У���ADE=90�㣬AD=DE��
�ߡ�AOB=90�㣬
���OAD+��ADO=��EDH+��ADO=90�㣬
���OAD=��EDH��
�ڡ�AOD�͡�DHE�У�
$\left\{\begin{array}{l}{��OAD=��EDH}\\{��AOD=��DHE}\\{AD=DE}\end{array}\right.$��
���AOD�ա�DHE��AAS����
��DH=AO=1��EH=DO=m��
��E��m+1��m����
��֤����
��x=m+1ʱ��y=x-1=m+1-1=m��
���mȡ��ֵ��E����ֱ��y=x-1��
��2����E��EH��x����H����ͼ2��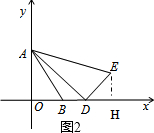
��Rt��ADE�У���ADE=90�㣬
�ߡ�AOB=90�㣬
���OAD=��EDH����ADO=��DEH��
���AOD�ס�DHE��
��DH��AO=EH��OD=DE��AD=1��$\sqrt{3}$��
��DH=1��EH=$\frac{{\sqrt{3}}}{3}m$��
��E��m+1��$\frac{{\sqrt{3}}}{3}m$����$y=\frac{{\sqrt{3}}}{3}x-\frac{{\sqrt{3}}}{3}$��
��3����Rt��AOB����������λ����Rt��CFG����ͼ3��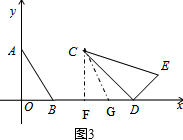
���ݣ�2���Ľ�𣬰ѣ�2���е�ֱ������������λ���ɣ�
��������ֱ�߽���ʽΪ$y=\frac{{\sqrt{3}}}{3}x-\sqrt{3}$��
����mȡ��ֵͬʱ����E����һ��ֱ���ϣ�
���� ������Ҫ����һ�κ������ۺ�Ӧ�ã��漰֪ʶ����ȫ�������ε��ж������ʡ����������ε��ж������ʡ���������ʽ�ȣ��ڣ�1����������ֱ����߶εij��ǽ���Ĺؼ����ڣ�2����֤����������������߶εij��ǽ���Ĺؼ����ڣ�3�������úã�2���Ľ����ǽ���Ĺؼ�������֪ʶ��϶࣬�ѶȽϴ��ۺ��Խ�ǿ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
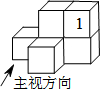 ��ͼ����6��ͬ����С��������ڳɵļ����壮�����С�1����������������ߺ����ü����壨������
��ͼ����6��ͬ����С��������ڳɵļ����壮�����С�1����������������ߺ����ü����壨������| A�� | ����ͼ�ı䣬����ͼ�ı� | B�� | ����ͼ�ı䣬����ͼ���� | ||
| C�� | ����ͼ���䣬����ͼ���� | D�� | ����ͼ���䣬����ͼ�ı� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
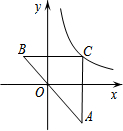 ��ͼ��Rt��ABC��б��AB��������ԭ�㣬��ֱ�DZ߷ֱ�ƽ���������ᣬ��C�ڷ���������$y=\frac{k}{x}$��ͼ���ϣ�����A��������Ϊ$-\frac{7}{2}$������B�ĺ�����Ϊ-2����k��ֵΪ7��
��ͼ��Rt��ABC��б��AB��������ԭ�㣬��ֱ�DZ߷ֱ�ƽ���������ᣬ��C�ڷ���������$y=\frac{k}{x}$��ͼ���ϣ�����A��������Ϊ$-\frac{7}{2}$������B�ĺ�����Ϊ-2����k��ֵΪ7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽�ȫ��ͬѧÿ������������ʱ�� | B�� | ѧУ��Ƹ��ʦ����ӦƸ��Ա���� | ||
| C�� | �˽���������Сѧ��ÿ����㻨Ǯ | D�� | �ÿ��Ϸɻ�ǰ�İ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -2 | C�� | 0 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com