
 如图,⊙O的直径AB=4,AC=AD,∠CAB=30°,点O到CD的距离OE=$\sqrt{2}$.
如图,⊙O的直径AB=4,AC=AD,∠CAB=30°,点O到CD的距离OE=$\sqrt{2}$. 分析 连接OC,在等腰△ACD中,顶角∠A=30°,易求得∠ACD=75°;根据等边对等角,可得:∠OCA=∠A=30°,由此可得∠OCD=45°,即△COE是等腰直角三角形,则OE=$\sqrt{2}$.
解答 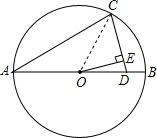 解:连接OC,
解:连接OC,
∵AC=AD,∠CAB=30°,
∴∠ACD=∠ADC=75°.
∵AO=OC,
∴∠OCA=∠CAB=30°;
∴∠OCD=45°,即△OCE是等腰直角三角形.
在等腰Rt△OCE中,
∵OC=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2;
∴OE=OC•sin45°=$\sqrt{2}$,即点O到CD的距离OE等于$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查的是垂径定理,等腰三角形的性质、三角形的内角和定理、解直角三角形等知识的应用,此题难度不大,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$-2 | B. | 5$\sqrt{5}$-5 | C. | 15-5$\sqrt{5}$ | D. | 0.618 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(40-x)=75 | B. | x(20-x)=75 | C. | x(x+40)=75 | D. | x(x+20)=75 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
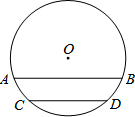 如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编)
如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com