
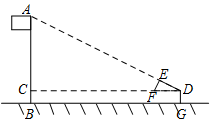
 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,且测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度.
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,且测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度. 分析 求出△ACD和△FED相似,根据相似三角形对应边成比例列式求出AC,再求出BC=DG,然后根据旗杆的高度AB=AC+BC代入数据计算即可得解.
解答 解:∵∠ADC=∠FDE,∠ACD=∠FED=90°,
∴△ACD∽△FED,
∴$\frac{AC}{EF}$=$\frac{CD}{DE}$,
即$\frac{AC}{0.25}$=$\frac{25}{0.5}$,
解得AC=12.5,
∵AB⊥BG,DG⊥BG,DC⊥AB,
∴∠ABG=∠BGD=∠DCB=90°,
∴四边形BGDC是矩形,
∴BC=DG=1.5,
∴AB=AC+BC=12.5+1.5=14米.
答:旗杆AB的高度是14米.
点评 本题考查了相似三角形的应用,矩形的判定与性质,主要利用了相似三角形对应边成比例.


科目:初中数学 来源: 题型:解答题
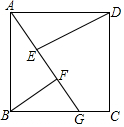 已知:如图,四边形ABCD是正方形,G是BC上的一点,DE⊥AG,BF⊥AG,垂足分别为E、F.
已知:如图,四边形ABCD是正方形,G是BC上的一点,DE⊥AG,BF⊥AG,垂足分别为E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
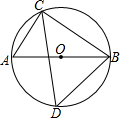 如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )| A. | CD=(AC+BC)sinθ | B. | CD=(AC+BC)cosθ | ||
| C. | CD=AC•cosθ+BC•sinθ | D. | CD=AC•sinθ+BC•cosθ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y3<y2<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有最大值-23 | B. | 有最小值-23 | C. | 有最大值23 | D. | 有最小值23 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com