
| A�� | �����ֵ-23 | B�� | ����Сֵ-23 | C�� | �����ֵ23 | D�� | ����Сֵ23 |
���� ͨ���䷽�ɵ�-3x2+12x-11=-3��x-2��2+23������֪����ֵ���
��� �⣺-3x2+12x-11=-3��x2-4x��+11
=-3��x2-4x+4-4��+11
=-3��x-2��2+12+11
=-3��x-2��2+23��
������xȡ��ʵ�������У�x-2��2��0��
��-3��x-2��2��0��
��-3��x-2��2+23��23��
������xȡ��ʵ������������ʽ-3x2+12x+11�����ֵ23��
��ѡ��C��
���� ���⿼�����䷽����Ӧ�ã�����ʱҪ�����䷽���IJ�����н��ע���ڱ��εĹ����в�Ҫ�ı�ʽ�ӵ�ֵ��


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
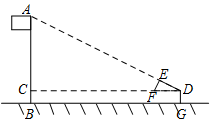 ��ͼ��ijУ��ѧ��ȤС���������Ƶ�ֱ��������Ӳֽ��DEF�������ٳ����AB�ĸ߶ȣ�����ͨ����������λ�ã�ʹб��DF����汣��ƽ�в�ʹֱ�DZ�DE����˶���A��ͬһֱ���ϣ���֪DE=0.5�ף�EF=0.25�ף��Ҳ��D������ľ���DG=1.5�ף�����˵�ˮƽ����DC=25�ף������AB�ĸ߶ȣ�
��ͼ��ijУ��ѧ��ȤС���������Ƶ�ֱ��������Ӳֽ��DEF�������ٳ����AB�ĸ߶ȣ�����ͨ����������λ�ã�ʹб��DF����汣��ƽ�в�ʹֱ�DZ�DE����˶���A��ͬһֱ���ϣ���֪DE=0.5�ף�EF=0.25�ף��Ҳ��D������ľ���DG=1.5�ף�����˵�ˮƽ����DC=25�ף������AB�ĸ߶ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
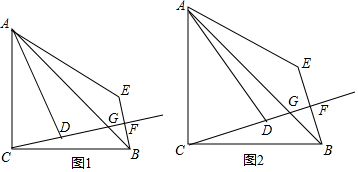
 ��ͼ����������ABCD�У�E��F�ֱ���AB��BC��һ�㣬EG��AF��H����CD�ڵ�G����֤��BE+BF=CG��
��ͼ����������ABCD�У�E��F�ֱ���AB��BC��һ�㣬EG��AF��H����CD�ڵ�G����֤��BE+BF=CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com