
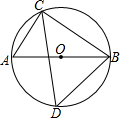
 如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )| A. | CD=(AC+BC)sinθ | B. | CD=(AC+BC)cosθ | ||
| C. | CD=AC•cosθ+BC•sinθ | D. | CD=AC•sinθ+BC•cosθ |
分析 连接AD,作BH⊥CD于H,根据圆周角定理得到∠ACB=∠ADB=90°,根据正弦、余弦的定义求出BD、BH,根据勾股定理求出DH,计算即可.
解答 解: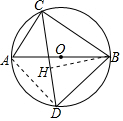 连接AD,作BH⊥CD于H,
连接AD,作BH⊥CD于H,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∴BD=AB•sin∠BAD=AB•sinθ,
在Rt△ACB中,AC2+BC2=AB2=$\frac{B{D}^{2}}{si{n}^{2}θ}$,
即BD2=AC2sin2θ+BC2sin2θ,
BH=BC•sinθ,CH=BC•cosθ,
DH=$\sqrt{B{D}^{2}-B{H}^{2}}$=AC•sinθ,
∴CD=CH+DH=AC•sinθ+BC•cosθ,
故选:D.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握圆周角定理、勾股定理、锐角三角函数的定义是解题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:选择题
| A. | 2b<C<2(a+b) | B. | a+b<C<3b | C. | 2a+b<C<a+2b | D. | 2(a+b)<C<a+3b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
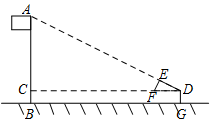 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,且测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度.
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,且测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
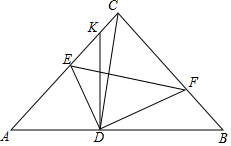 如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.
如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com