
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点为A,B(点A 在点B的左侧).
轴的交点为A,B(点A 在点B的左侧).
(1)求点A,B的坐标;
(2)横、纵坐标都是整数的点叫整点.
①直接写出线段AB上整点的个数;
②将抛物线![]() 沿
沿![]() 翻折,得到新抛物线,直接写出新抛物线在
翻折,得到新抛物线,直接写出新抛物线在![]() 轴上方的部分与线段
轴上方的部分与线段![]() 所围成的区域内(包括边界)整点的个数.
所围成的区域内(包括边界)整点的个数.
【答案】(1)点A的坐标为(-1,0),点B的坐标为(3,0)(2)①5;②6.
【解析】
(1)根据x轴上的点的坐标特征即y=0,可得关于x的方程,解方程即可;
(2)①直接写出从-1到3的整数的个数即可;
②先确定新抛物线的解析式,进而可得其顶点坐标,再结合函数图象解答即可.
解:(1)在![]() 中 ,令y=0,
中 ,令y=0,![]() ,解得:
,解得:![]() ,
,
∴点A的坐标为(-1,0),点B的坐标为(3,0);
(2)①线段AB之间横、纵坐标都是整数的点有(-1,0)、(0,0)、(1,0)、(2,0)、(3,0).
∴线段AB上一共有5个整点;
②抛物线![]() 沿
沿![]() 翻折,得到的新抛物线是
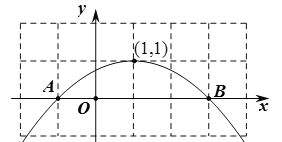
翻折,得到的新抛物线是![]() ,如图,其顶点坐标是(1,1),
,如图,其顶点坐标是(1,1),
观察图象可知:线段AB上有5个整点,顶点为1个整点,新抛物线在![]() 轴上方的部分与线段
轴上方的部分与线段![]() 所围成的区域内(包括边界)共6个整点.
所围成的区域内(包括边界)共6个整点.


科目:初中数学 来源: 题型:
【题目】如图将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,
(1)求证:△AME∽△BEC.
(2)若△EMC∽△AME,求AB与BC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.过点D作DG∥BE,交BC于点G,连接FG交BD于点O.若AB=6,AD=8,则DG的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课堂上同学们借助两个直角三角形纸板进行探究,直角三角形纸板如图所示,分别为Rt△ABC和Rt△DEF,其中∠A=∠D=90°,AC=DE=2cm. 当边AC与DE重合,且边AB和DF在同一条直线上时:

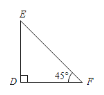
(1)在下边的图形中,画出所有符合题意的图形;

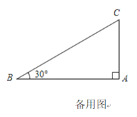
(2)求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一颗质地均匀的骰子已连续抛掷了2000次,其中抛掷出5点的次数最少,则第2001次一定抛掷出5点
B.抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等
C.明天降雨的概率是80%,表示明天有80%的时间降雨
D.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
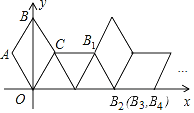
【题目】如图,在坐标系中放置一菱形![]() ,已知
,已知![]() ,
,![]() ,先将菱形
,先将菱形![]() 沿
沿![]() 轴的正方向无滑动翻转,每次翻转
轴的正方向无滑动翻转,每次翻转![]() ,连续翻转2019次,点
,连续翻转2019次,点![]() 的落点依次为
的落点依次为![]() ,
,![]() ,
,![]() ,…,则
,…,则![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
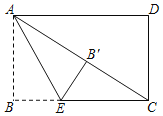
【题目】如图,在矩形ABCD中,AB=1,BC=2,点E在边BC上,将△ABE沿AE折叠,点B恰好落在对角线AC上的点B′处.则线段BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,共获利3192元.问第二次降价后售出该种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两点M(x1,y1),N(x2,y2),则线段MN的中点K(x,y)的坐标公式为:x=![]() ,y=
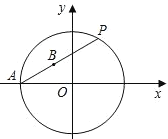
,y=![]() . 如图,已知点O为坐标原点,点A(﹣3,0),⊙O经过点A,点B为弦PA的中点.若点P(a,b),则有a,b满足等式:a2+b2=9.设B(m,n),则m,n满足的等式是( )
. 如图,已知点O为坐标原点,点A(﹣3,0),⊙O经过点A,点B为弦PA的中点.若点P(a,b),则有a,b满足等式:a2+b2=9.设B(m,n),则m,n满足的等式是( )
A.m2+n2=9B.(![]() )2+(
)2+(![]() )2=9
)2=9
C.(2m+3)2+(2n)2=3D.(2m+3)2+4n2=9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com