
【题目】某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,共获利3192元.问第二次降价后售出该种商品多少件?
【答案】(1)这种商品每次降价的百分率为10%;(2)第二次降价后售出这种商品78件.
【解析】
(1)设该商品每次降价的百分率为![]() ,根据“两次降价后的售价=原价×(1-
,根据“两次降价后的售价=原价×(1-![]() ”,即可得出关于x的一元二次方程,解方程即可得出结论.
”,即可得出关于x的一元二次方程,解方程即可得出结论.
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品(100-m)件,根据“总利润=第一次降价后的单件利润×销售数量+第二次降价后的单件利润×销售数量”,即可得出关于m的一元一次方程,解之即可得出结论.
(1)设这种商品每次降价的百分率为x,根据题题意得
400×(1-x)2=324,
解得:x1=10%,x2=1.9(不合题意,舍去).
答:这种商品每次降价的百分率为10%.
(2)设第二次降价后售出该种商品m件,则第一次降价后售出该种商品(100-m)件,
第一次降价后的单件利润为400×(1-10%)-300=60(元/件) ,
第二次降价后的单件利润为324-300=24(元/件) ,
依题意,得![]() ,
,
解得:![]() ,
,
答:第二次降价后售出这种商品78件.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,BC平分∠ABD
(1) 若∠A=100°,则∠1的度数为_________
(2) 判断AC与BD的位置关系,并证明你的结论

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点为A,B(点A 在点B的左侧).
轴的交点为A,B(点A 在点B的左侧).
(1)求点A,B的坐标;
(2)横、纵坐标都是整数的点叫整点.
①直接写出线段AB上整点的个数;
②将抛物线![]() 沿
沿![]() 翻折,得到新抛物线,直接写出新抛物线在
翻折,得到新抛物线,直接写出新抛物线在![]() 轴上方的部分与线段
轴上方的部分与线段![]() 所围成的区域内(包括边界)整点的个数.
所围成的区域内(包括边界)整点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,在平行四边形ABCD中,点E是BC边的中点,连结AE,点F是线段AE上一点,连结BF并延长,交射线CD于点G.若AF:EF=4:1,求![]() 的值.
的值.
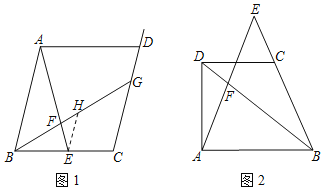
(1)尝试探究:
如图1,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是.CG和EH的数量关系是,因此![]() = .
= .
(2)类比延伸:
在原题的条件下,若把“AF:EF=4:1”改为“AF:EF=n:1”(n>0),求![]() 的值.(用含有n的式子表示)
的值.(用含有n的式子表示)
(3)拓展迁移:
如图2,在四边形ABCD中,CD∥AB,点E是BC的延长线上的一点,AE与BD相交于点F.若AB:CD=a:1(a>0),BC:BE=b:1(b>0),则![]() = .(直接用含有a、b的式子表示,不写解答过程)
= .(直接用含有a、b的式子表示,不写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 经过
经过![]() 两点,交
两点,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
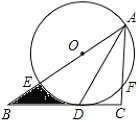
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径是
的半径是![]() ,
,![]() 是弧
是弧![]() 的中点,求阴影部分的面积(结果保留
的中点,求阴影部分的面积(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
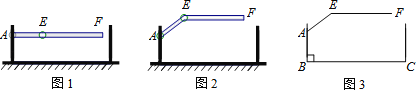
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB=6,AC=3,∠BAC=60°,![]() 为⊙O上的一段弧,且∠BOC=60°,分别在
为⊙O上的一段弧,且∠BOC=60°,分别在![]() 、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为__________
、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为__________
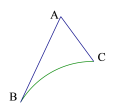
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的两个动点,且
上的两个动点,且![]() ,过点
,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .有以下结论:①
.有以下结论:①![]() ;②当点
;②当点![]() 与点
与点![]() 重合时,
重合时,![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com