
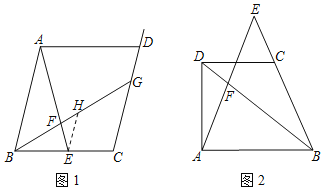
【题目】问题:如图1,在平行四边形ABCD中,点E是BC边的中点,连结AE,点F是线段AE上一点,连结BF并延长,交射线CD于点G.若AF:EF=4:1,求![]() 的值.
的值.
(1)尝试探究:
如图1,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是.CG和EH的数量关系是,因此![]() = .
= .
(2)类比延伸:
在原题的条件下,若把“AF:EF=4:1”改为“AF:EF=n:1”(n>0),求![]() 的值.(用含有n的式子表示)
的值.(用含有n的式子表示)
(3)拓展迁移:
如图2,在四边形ABCD中,CD∥AB,点E是BC的延长线上的一点,AE与BD相交于点F.若AB:CD=a:1(a>0),BC:BE=b:1(b>0),则![]() = .(直接用含有a、b的式子表示,不写解答过程)
= .(直接用含有a、b的式子表示,不写解答过程)
【答案】(1)2;(2)![]() ;(3)ab.
;(3)ab.
【解析】
(1)本问体现“特殊”的情形,![]() =4是一个确定的数值.根据平行线构造相似三角形,利用相似三角形性质,分别将各相关线段均统一用EH来表示,最后求得比值;
=4是一个确定的数值.根据平行线构造相似三角形,利用相似三角形性质,分别将各相关线段均统一用EH来表示,最后求得比值;
(2)本问体现“一般”的情形,![]() =n不再是一个确定的数值,但(1)问中的解题方法依然适用,如答图2所示.
=n不再是一个确定的数值,但(1)问中的解题方法依然适用,如答图2所示.
(3)本问体现“类比”与“转化”的情形,将(1)(2)问中的解题方法推广转化到梯形中,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD,根据平行线构造相似三角形,利用相似三角形性质,分别将各相关线段均统一用EH来表示,最后求得比值,如答图3所示.
解:(1)∵EH∥AB
∴△ABF∽△EHF,
∴![]() =
=![]() =4,
=4,
∴AB=4EH.
∵平行四边形ABCD中,EH∥AB,
∴EH∥CD,
∴△BEH∽△BCG.
∴![]() =
=![]() =2,
=2,
∴CG=2EH.
∴![]() =
=![]() =
=![]() =2.
=2.
故答案为:2.
(2)如图2所示,作EH∥AB交BG于点H,
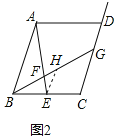
则△EFH∽△AFB.
∴![]() =
=![]() =n,
=n,
∴AB=nEH.
∵AB=CD,
∴CD=nEH.
∵EH∥AB∥CD,
∴△BEH∽△BCG.
∴![]() =
=![]() =2,
=2,
∴CG=2EH.
∴![]() =
=![]() =
=![]() .
.
(3)如图3所示,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD.
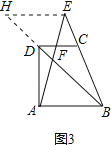
∵EH∥CD,
∴△BCD∽△BEH,
∴![]() =
=![]() =b,
=b,
∴CD=bEH.
又![]() =a,
=a,
∴AB=aCD=abEH.
∵EH∥AB,
∴△ABF∽△EHF,
∴![]() =
=![]() =
=![]() =ab,
=ab,
故答案为:ab.


科目:初中数学 来源: 题型:
【题目】如图,某幢建筑物从2.25米高的窗口![]() 用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点
用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点![]() 离墙1米,离地面3米,则水流下落点
离墙1米,离地面3米,则水流下落点![]() 离墙的距离
离墙的距离![]() 是( )
是( )
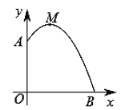
A.2.5米B.3米C.3.5米D.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课堂上同学们借助两个直角三角形纸板进行探究,直角三角形纸板如图所示,分别为Rt△ABC和Rt△DEF,其中∠A=∠D=90°,AC=DE=2cm. 当边AC与DE重合,且边AB和DF在同一条直线上时:

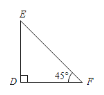
(1)在下边的图形中,画出所有符合题意的图形;

(2)求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
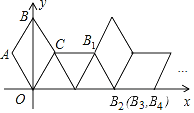
【题目】如图,在坐标系中放置一菱形![]() ,已知
,已知![]() ,
,![]() ,先将菱形
,先将菱形![]() 沿
沿![]() 轴的正方向无滑动翻转,每次翻转
轴的正方向无滑动翻转,每次翻转![]() ,连续翻转2019次,点
,连续翻转2019次,点![]() 的落点依次为
的落点依次为![]() ,
,![]() ,
,![]() ,…,则
,…,则![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
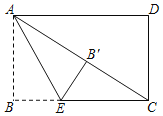
【题目】如图,在矩形ABCD中,AB=1,BC=2,点E在边BC上,将△ABE沿AE折叠,点B恰好落在对角线AC上的点B′处.则线段BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,共获利3192元.问第二次降价后售出该种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
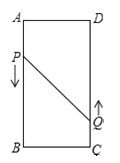
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com