【题目】如图，要使平行四边形ABCD成为矩形，需添加的条件是（ ）
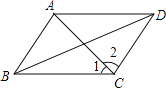
A.AB＝BCB.AC⊥BDC.∠ABC＝90°D.∠1＝∠2
【答案】C
【解析】
根据矩形的判定定理（①有一个角是直角的平行四边形是矩形，②有三个角是直角的四边形是矩形，③对角线相等的平行四边形是矩形）逐一判断即可．
A、根据AB＝BC和平行四边形ABCD不能得出四边形ABCD是矩形，故本选项错误；
B、∵四边形ABCD是平行四边形，
∴当AC⊥BD时四边形ABCD是菱形，故本选项错误；
C、∵四边形ABCD是平行四边形，AC⊥BD，
∴平行四边形ABCD是菱形，不能推出四边形ABCD是矩形，故本选项错误；
D、∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠2＝∠ACB，
∵∠1＝∠2，
∴∠1＝∠ACB，
∴AB＝BC，
∴四边形ABCD是菱形，不能推出四边形ABCD是矩形，故本选项错误；
故选：C．
名师金手指领衔课时系列答案科目：初中数学 来源： 题型：
【题目】问题：如图1，在平行四边形ABCD中，点E是BC边的中点，连结AE，点F是线段AE上一点，连结BF并延长，交射线CD于点G．若AF：EF＝4：1，求
的值．
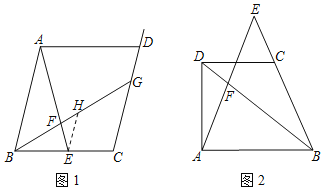
（1）尝试探究：
如图1，过点E作EH∥AB交BG于点H，则AB和EH的数量关系是．CG和EH的数量关系是，因此＝ ．
（2）类比延伸：
在原题的条件下，若把“AF：EF＝4：1”改为“AF：EF＝n：1”（n＞0），求的值．（用含有n的式子表示）
（3）拓展迁移：
如图2，在四边形ABCD中，CD∥AB，点E是BC的延长线上的一点，AE与BD相交于点F．若AB：CD＝a：1（a＞0），BC：BE＝b：1（b＞0），则
＝ ．（直接用含有a、b的式子表示，不写解答过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示,AB＝6,AC＝3,∠BAC＝60°,
为⊙O上的一段弧,且∠BOC＝60°,分别在、线段AB和AC上选取点P、E、F,则PE＋EF＋FP的最小值为__________
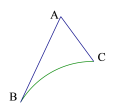
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并完成相应的任务.
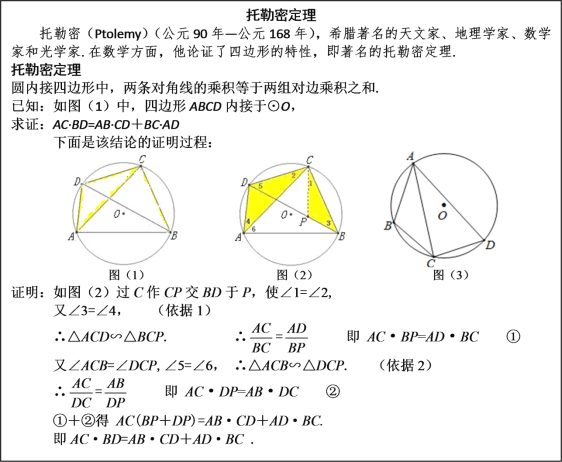
任务：
（1）上述证明过程中的“依据1”和“依据2”分别指什么？
依据1：
依据2：
（2）当圆内接四边形ABCD是矩形时，托勒密定理就是我们非常熟知的一个定理： （请写出定理名称）.
（3）如图（3），四边形ABCD内接于⊙O，AB=3，AD=5，∠BAD=60°，点C是弧BD的中点，求AC的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某新建火车站站前广场需要绿化的面积为46000米2，施工队在绿化了22000米2后，将每天的工作量增加为原来的1.5倍，结果提前4天完成了该项绿化工程．
（1）该项绿化工程原计划每天完成多少米2？
（2）该项绿化工程中有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米2，两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，
，
，
是线段
上的两个动点，且
，过点，分别作
，
的垂线相交于点
，垂足分别为
，
.有以下结论：①
；②当点与点
重合时，
；③
；④
.其中正确的结论有（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
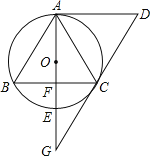
【题目】如图，菱形ABCD，∠D＝60°，△ABC内接于⊙O，⊙O的直径AE交BC于F，DC的延长线交AE的延长线于点G．
（1）求证：DG与⊙O相切；
（2）连接DF，求tan∠FDC的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
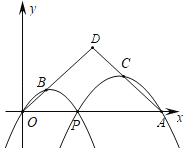
【题目】如图，已知点A(12，0)，O为坐标原点，P是线段OA上任一点(不含端点O、A).二次函数y1的图象过P、O两点.二次数y2的图象过P、A两点，它的开口均向下，顶点分别为B、C.射线OB与射线AC相交于点D.用当OD＝AD＝9时，这两个二次函数的最大值之和等于______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
