
【题目】阅读下列材料,并完成相应的任务.
任务:
(1)上述证明过程中的“依据1”和“依据2”分别指什么?
依据1:
依据2:
(2)当圆内接四边形ABCD是矩形时,托勒密定理就是我们非常熟知的一个定理: (请写出定理名称).
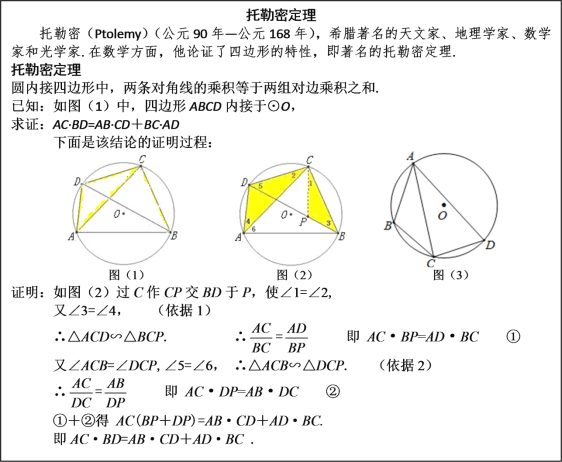
(3)如图(3),四边形ABCD内接于⊙O,AB=3,AD=5,∠BAD=60°,点C是弧BD的中点,求AC的长.
【答案】(1)同弧所对的圆周角相等;两角分别对应相等的两个三角形相似(2)勾股定理(3) AC =![]()
【解析】
(1)根据圆周角定理的推论以及三角形相似的判定定理,即可得到答案;
(2)根据矩形的性质和托勒密定理,即可得到答案;
(3)连接BD,过点C作CE⊥BD于点E.由四边形ABCD内接于⊙O,点C是弧BD的中点,可得BCD是底角为30°的等腰三角形,进而得BD=2 DE=![]() CD,结合托勒密定理,列出方程,即可求解.
CD,结合托勒密定理,列出方程,即可求解.
(1)依据1指的是:同弧所对的圆周角相等;
依据2指的是:两角分别对应相等的两个三角形相似 .
故答案是:同弧所对的圆周角相等;两角分别对应相等的两个三角形相似;
(2)∵当圆内接四边形ABCD是矩形时,
∴AC=BD,BC=AD,AB=CD,
∵由托勒密定理得:AC·BD=AB·CD+BC·AD,
∴![]() .
.
故答案是:勾股定理;
(3)如图,连接BD,过点C作CE⊥BD于点E.
∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD =180°,
∵∠BAD=60°,
∴∠BCD =120°,
∵点C是弧BD的中点,
∴ 弧BC=弧CD,
∴ BC =CD,
∴∠CBD =30°.
在Rt△CDE中,DE=CD·cos30°,
∴DE=![]() CD ,
CD ,
∴ BD=2 DE=![]() CD.
CD.
由托勒密定理得: AC·BD=AB·CD+BC·AD.
∴AC·![]() CD=3CD+5CD.
CD=3CD+5CD.
∴AC =![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
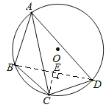
【题目】如图,在坐标系中放置一菱形![]() ,已知
,已知![]() ,
,![]() ,先将菱形
,先将菱形![]() 沿
沿![]() 轴的正方向无滑动翻转,每次翻转
轴的正方向无滑动翻转,每次翻转![]() ,连续翻转2019次,点
,连续翻转2019次,点![]() 的落点依次为
的落点依次为![]() ,
,![]() ,
,![]() ,…,则
,…,则![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
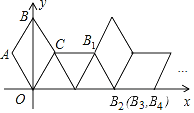
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
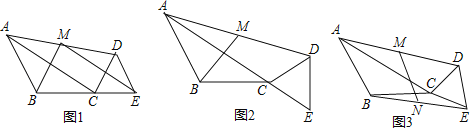
【题目】在△ABC中,AB=BC=2![]() ,∠ABC=120°,△CDE为等边三角形,CD=2,连接AD,M为AD中点.
,∠ABC=120°,△CDE为等边三角形,CD=2,连接AD,M为AD中点.
(1)如图1,当B,C,E三点共线时,请画出△EDM关于点M的中心对称图形,并证明BM⊥ME;
(2)如图2,当A,C,E三点共线时,求BM的长;
(3)如图3,取BE中点N,连MN,将△CDE绕点C旋转,直接写出旋转过程中线段MN的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两点M(x1,y1),N(x2,y2),则线段MN的中点K(x,y)的坐标公式为:x=![]() ,y=
,y=![]() . 如图,已知点O为坐标原点,点A(﹣3,0),⊙O经过点A,点B为弦PA的中点.若点P(a,b),则有a,b满足等式:a2+b2=9.设B(m,n),则m,n满足的等式是( )
. 如图,已知点O为坐标原点,点A(﹣3,0),⊙O经过点A,点B为弦PA的中点.若点P(a,b),则有a,b满足等式:a2+b2=9.设B(m,n),则m,n满足的等式是( )
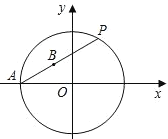
A.m2+n2=9B.(![]() )2+(
)2+(![]() )2=9
)2=9
C.(2m+3)2+(2n)2=3D.(2m+3)2+4n2=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为______km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为______km.

查看答案和解析>>
科目:初中数学 来源: 题型:
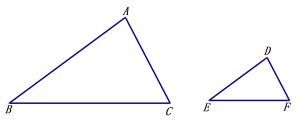
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com