Question

6．如图，△ABC内接于⊙O，D是弧BC的中点，OD交BC于点H，且OH=DH，连接AD，过点B作BE⊥AD于点E，连接EH，BF⊥AC于M，若AC=5，EH=$\frac{3}{2}$，则AF=$\frac{7\sqrt{3}}{3}$．

Answer 1

分析 如图，延长BE交AC的延长线于N，连接OB、OC、BD．首先证明AB=AN，推出AB=8，再证明△OBD是等边三角形，推出∠BAC=60°，利用勾股定理分别求出BM、BC，再利用△AMF∽△BMC，得$\frac{AF}{BC}$=$\frac{AM}{BM}$，延长即可解决问题．

解答 解：如图，延长BE交AC的延长线于N，连接OB、OC、BD．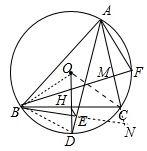

∵$\widehat{BD}$=$\widehat{DC}$，
∴∠EAB=∠EAN，
∵AD⊥BN，
∴∠AEB=∠AEN=90°，
∴∠ABE+∠BAE=90°，∠N+∠EAN=90°，
∴∠ABE=∠N，
∴AB=AN，
∴BE=EN，
∵OD⊥BC，
∴BH=HC，
∴CN=2EH，
∴AB=AN=AC+CN=8，
∵OH=HD，BH⊥OD，
∴BO=BD=OD，
∴∠BOD=∠DOC=60°，
∴∠BAC=$\frac{1}{2}$∠BOC=60°，
在Rt△AMB中，AM=$\frac{1}{2}$AB=4，BM=4$\sqrt{3}$，
在Rt△BMC中，BC=$\sqrt{B{M}^{2}+C{M}^{2}}$=$\sqrt{（4\sqrt{3}）^{2}+{1}^{2}}$=7，
∵∠MAF=∠MBC，∠AMF=∠BMC，
∴△AMF∽△BMC，
∴$\frac{AF}{BC}$=$\frac{AM}{BM}$，
∴$\frac{AF}{7}$=$\frac{4}{4\sqrt{3}}$，
∴AF=$\frac{7\sqrt{3}}{3}$．
故答案为$\frac{7\sqrt{3}}{3}$．

点评 此题考查了圆周角定理、垂径定理、全等三角形的判定、勾股定理，相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，注意掌握数形结合思想的应用，属于中考填空题中的压轴题．