
 ���ɶ�������������ΰ��Ķ���֮һ�����ô���˼���������������Ҫ���ߣ�Ҳ�����ν�ϵ�Ŧ��������ʦ���ϰ��꼶���ӹ��ɶ�����ͼ�������ϵ����չ��һ����չ��ʱ����ѧ�������������ݰ�������������ƺ��������£�����Ϊ�������˵��㣬�����˼������������⣺
���ɶ�������������ΰ��Ķ���֮һ�����ô���˼���������������Ҫ���ߣ�Ҳ�����ν�ϵ�Ŧ��������ʦ���ϰ��꼶���ӹ��ɶ�����ͼ�������ϵ����չ��һ����չ��ʱ����ѧ�������������ݰ�������������ƺ��������£�����Ϊ�������˵��㣬�����˼������������⣺���� ����̽������1�����ۣ�S1+S2=S3������Բ�����ʽ�Լ����ɶ�������֤����
��2���ȱ������Σ����õȱ������ε�����Լ����ɶ�������֤����
��չӦ�ã���1����������̽���еĽ��ۼ��ɽ�����⣮
��2������S1+S2=$\frac{1}{2}$�У�AB��2+$\frac{1}{2}$�У�$\frac{1}{2}$AC��2-$\frac{1}{2}$�У�$\frac{1}{2}$BC��2+S��ABC=$\frac{1}{8}$�У�BC2+AC2-AB2��+S��ABC=S��ABC���㼴�ɣ�
��� �⣺����̽������1�����ۣ�S1+S2=S3���������£�
��S3=$\frac{��}{8}$c2��S2=$\frac{��}{8}$b2��S1=$\frac{��}{8}$a2��a2+b2=c2��
��S1+S2=S3��
�ʴ�ΪS1+S2=S3��
��2���ȱ������λ����ֱ�������Σ�
��ͼ3�У���ֱ�������ε�������a��b��cΪ�ߣ��������ȱ������Σ���ͼ��ʾ��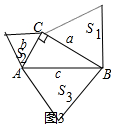
��S1=$\frac{\sqrt{3}}{4}$a2��S2=$\frac{\sqrt{3}}{4}$b2��S3=$\frac{\sqrt{3}}{4}$c2��a2+b2=c2��
��S2+S3=S1��
����������ʱ֤���������ƣ�
�ʴ�Ϊ�ȱ������λ����ֱ�������Σ�
��չӦ�ã���1����ͼ2�У���S1+S2=S3��S3=$\frac{��}{8}$c2=$\frac{��}{8}$��16=2�У�
�ʴ�Ϊ2�У�
2���⣺��ͼ5�У�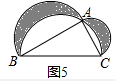
��ABC����AB2+AC2=BC2
��S1+S2=$\frac{1}{2}$��AB��2+$\frac{1}{2}$��$\frac{1}{2}$AC��2-$\frac{1}{2}$��$\frac{1}{2}$BC��2+S��ABC=$\frac{1}{8}$��BC2+AC2-AB2��+S��ABC=S��ABC=$\frac{1}{2}$��3��4=6��
�ʴ�Ϊ6��
���� ������Ҫ�漰��֪ʶ�㣺�����Ρ������Ρ�Բ����������Լ����ɶ�����Ӧ�ã�����ؼ����������չ��ɶ����Ĺ�ʽ��ѧ���ø������Ӱ��������������п��������ͣ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017����Ͻ����п���ѧģ���Ծ���2���������棩 ���ͣ���ѡ��
��ƽ��ֱ������ϵ��ֱ��y=x+2�뷴�������� ��ͼ����Ψһ�����㣬��ֱ��y=x+m�뷴��������
��ͼ����Ψһ�����㣬��ֱ��y=x+m�뷴�������� ��ͼ����2�������㣬��m��ȡֵ��Χ�ǣ� ��
��ͼ����2�������㣬��m��ȡֵ��Χ�ǣ� ��
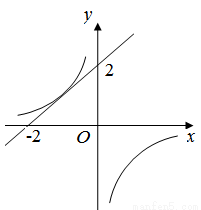
A. m��2 B. ��2��m��2
C. m����2 D. m��2��m����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ���Ĵ�ʡ�ϳ��ж���ѧ�ڰ��꼶�ڶ����¿���ѧ�Ծ��������棩 ���ͣ������
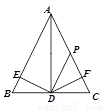
��ͼ����ABC�У�AP=DP��DE=DF��DE��AB��E��DF��AC��F�������н��ۣ���.ADƽ�֡�BAC����.��BED�ա�FPD����.DP��AB����.DF��PC�Ĵ�ֱƽ���ߣ�������ȷ����= _________ .��д��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�����߶�AC=1������C��CD��AC������ʹCD=$\frac{1}{2}$AC������AD���Ե�DΪԲ�ģ�DC�ij�Ϊ�뾶��������AD�ڵ�E�����Ե�AΪԲ�ģ�AE�ij�Ϊ�뾶��������AC�ڵ�B����AB�ij�Ϊ��������
��ͼ�����߶�AC=1������C��CD��AC������ʹCD=$\frac{1}{2}$AC������AD���Ե�DΪԲ�ģ�DC�ij�Ϊ�뾶��������AD�ڵ�E�����Ե�AΪԲ�ģ�AE�ij�Ϊ�뾶��������AC�ڵ�B����AB�ij�Ϊ��������| A�� | $\frac{2\sqrt{5}-1}{5}$ | B�� | $\frac{\sqrt{5}-1}{2}$ | C�� | $\frac{\sqrt{5}-1}{4}$ | D�� | $\frac{\sqrt{5}+1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����һ���߳�Ϊ2�������κ�һ��ֱ�DZ�Ϊ2�ĵ���ֱ��������ƴ��һ����ɵ�ͼ�Σ����ܰ����ֳ�4��ȫ�ȵ�ͼ�������ܻ����ָ��ߣ�
��ͼ����һ���߳�Ϊ2�������κ�һ��ֱ�DZ�Ϊ2�ĵ���ֱ��������ƴ��һ����ɵ�ͼ�Σ����ܰ����ֳ�4��ȫ�ȵ�ͼ�������ܻ����ָ��ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
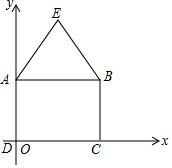 ��ͼ��ʾ���ڳ�����ABCD�У���֪AB=6��AD=4���ڳ�����ABCD�⻭��ABE��ʹAE=BE=5���뽨���ʵ���ƽ��ֱ������ϵ�����������������꣮
��ͼ��ʾ���ڳ�����ABCD�У���֪AB=6��AD=4���ڳ�����ABCD�⻭��ABE��ʹAE=BE=5���뽨���ʵ���ƽ��ֱ������ϵ�����������������꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�ڽ��ڡ�O��D�ǻ�BC���е㣬OD��BC�ڵ�H����OH=DH������AD������B��BE��AD�ڵ�E������EH��BF��AC��M����AC=5��EH=$\frac{3}{2}$����AF=$\frac{7\sqrt{3}}{3}$��
��ͼ����ABC�ڽ��ڡ�O��D�ǻ�BC���е㣬OD��BC�ڵ�H����OH=DH������AD������B��BE��AD�ڵ�E������EH��BF��AC��M����AC=5��EH=$\frac{3}{2}$����AF=$\frac{7\sqrt{3}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y2=4 | B�� | 2+$\frac{y}{2}$=6 | C�� | x2+x+1=0 | D�� | x-2y=1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com