
已知,如图,在 Rt△ABC 中,∠ACB=90°,AC=BC,点 E、F 分别是斜边 AB 上的两点,且∠FCE=45°.
(1)现将 CF 绕点 C 顺时针旋转 90°到 CD,连结 AD.求证:AD=BF. 若 EF=10,BF=8.求 AE 的长及△ABC 的面积.
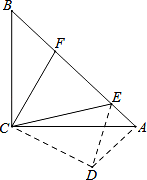
【考点】旋转的性质;全等三角形的判定与性质;勾股定理.
【分析】(1)证明△BCF≌△ACD,根据全等三角形的对应边相等即可证得; 首先证明△ECF≌△ECD,则 ED=EF,然后在直角△ADE 中利用勾股定理求得 AE 的长,则 AB 的 长即可求得,然后利用三角函数求得 AC 和 BC 的长,利用三角形的面积公式求解.
 【解答】(1)证明:在△BCF 和△ACD 中,
【解答】(1)证明:在△BCF 和△ACD 中,
,
∴△BCF≌△ACD,
∴AD=BF,∠CAD=∠CBA=45°.
 解:∵在△ECF 和△ECD 中,
解:∵在△ECF 和△ECD 中,
,
∴△ECF≌△ECD,
∴ED=EF,
 则在 Rt△DAE 中,由勾股定理可得:AE= =6,
则在 Rt△DAE 中,由勾股定理可得:AE= =6,


科目:初中数学 来源: 题型:
如图,已知线段 AB,请用尺规按下列要求作图(不写作法,保留作图痕迹):
(1)延长线段 AB 到 C,使 BC=AB; 延长线段 BA 到 D,使 AD=AC.
如果 AB=2cm,那么 AC= cm,BC= cm,CD= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲组的 4 名工人 3 月份完成的总工作量比此月人均定额的 4 倍多 20 件,乙组的 5 名工人 3 月份
完成的总工作量比此月人均定额的 6 倍少 20 件.
(1)如果两组工人实际完成的此月人均工作量相等,那么此月人均定额是多少件? 如果甲组工人实际完成的此月人均工作量比乙组的多 2 件,则此月人均定额是多少件?
(3)如果甲组工人实际完成的此月人均工作量比乙组的少 2 件,则此月人均定额是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,下列不正确的几何语句是
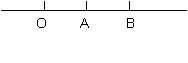 A. 直线AB与直线BA是同一条直线
A. 直线AB与直线BA是同一条直线
B. 射线OA与射线OB是同一条射线
C. 射线OA与射线AB是同一条射线
D. 线段AB与线段BA是同一条线段
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com