
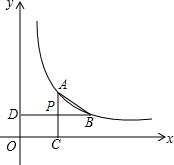
 如图,已知点A、B在双曲线y=$\frac{k}{x}$ (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
如图,已知点A、B在双曲线y=$\frac{k}{x}$ (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.分析 (1)根据点P是AC的中点得到点A的横坐标是m,结合反比例函数图象上点的坐标特征来求点B的坐标;
(2)根据点P的坐标得到点P是BD的中点,所以由“对角线互相垂直平分的四边形是菱形”得到四边形ABCD是菱形;
(3)由△ABP的面积为3,知BP•AP=6.根据反比例函数 y=kx中k的几何意义,知本题k=OC•AC,由反比例函数的性质,结合已知条件P是AC的中点,得出OC=BP,AC=2AP,进而求出k的值.
解答 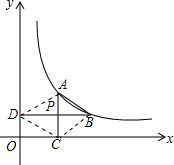 解:(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
解:(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
∴点B的横坐标是2m.
又∵点B在双曲线y=$\frac{k}{x}$ (x>0)上,
∴B(2m,$\frac{k}{2m}$).
(2)连接AD、CD、BC;
∵AC⊥x轴于C,BD⊥y轴于点D,
∴AC⊥BD;
∵A(m,$\frac{k}{m}$),B(2m,$\frac{k}{2m}$),
∴P(m,$\frac{k}{2m}$),
∴PD=PB,
又AP=PC,
∴四边形ABCD是菱形;
(3)∵△ABP的面积为 $\frac{1}{2}$•BP•AP=3,
∴BP•AP=6,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A、B都在双曲线y=$\frac{k}{x}$(x>0)上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴k=OC•AC=BP•2AP=12.
∴该双曲线的解析式是:y=$\frac{12}{x}$
点评 主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
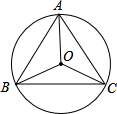 如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )| A. | 60° | B. | 150° | C. | 180° | D. | 240° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售出件数 | 7 | 6 | 3 | 5 | 4 | 5 |
| 售价/元 | +3 | +2 | +1 | 0 | -1 | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com