
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
���� ���ݷ�ʽ�ķ��ӷ�ĸ�����Ի����ͬһ����Ϊ�����ʽ����ʽ��ֵ���䣬�ɵô𰸣�
��� �⣺��$\frac{x}{3{x}^{2}}$=$\frac{1}{3x}$���ӷ�ĸ������x���ʢ���ȷ��
��$\frac{a+m}{b+m}$=$\frac{a}{b}$���ӷ�ĸ����m���ʢڴ���
��$\frac{2}{2+a}$=$\frac{1}{1+a}$���ӷ�ĸ����1���ʢ۴���
��$\frac{2+xy}{xy+2}$=1���ӷ�ĸ�����ԣ�xy+2�����ʢ���ȷ��
��$\frac{{a}^{2}-1}{a+1}$=a-1���ӷ�ĸ�����ԣ�a+1�����ʢ���ȷ��
��$\frac{-��x-y��}{��x-y��^{2}}$=-$\frac{1}{x-y}$���ӷ�ĸ�����ԣ�x-y�����ʢ���ȷ��
��ѡ��C��
���� ���⿼���˷�ʽ�������ʣ���ʽ�ķ��ӷ�ĸ�����Ի����ͬһ����Ϊ�����ʽ����ʽ��ֵ���䣬��ע��ʽ�ķ��ӷ�ĸ���ӻ��ͬһ��������ʽ��ֵ�����仯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
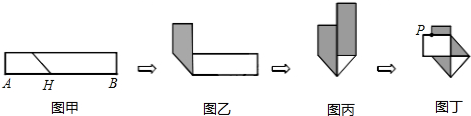
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
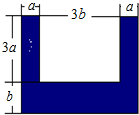 ��ͼ��
��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
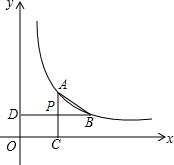 ��ͼ����֪��A��B��˫����y=$\frac{k}{x}$ ��x��0���ϣ�AC��x����C��BD��y���ڵ�D��AC��BD���ڵ�P��P��AC���е㣮
��ͼ����֪��A��B��˫����y=$\frac{k}{x}$ ��x��0���ϣ�AC��x����C��BD��y���ڵ�D��AC��BD���ڵ�P��P��AC���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com