
【题目】如图,点![]() 是
是![]() 直径
直径![]() 上的一点,过
上的一点,过![]() 作直线
作直线![]() ,分别交
,分别交![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,并将线段
,并将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,分别交
,分别交![]() 和
和![]() 于
于![]() ,
,![]() ,连接
,连接![]() .
.
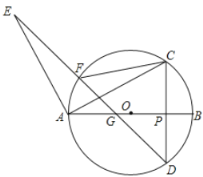
(Ⅰ)求证:![]() ;
;
(Ⅱ)若点![]() 在直径
在直径![]() 上运动(不与点
上运动(不与点![]() ,
,![]() 重合),其它条件不变,请问
重合),其它条件不变,请问![]() 是否为定值?若是,请求出其值;若不是,请说明理由.
是否为定值?若是,请求出其值;若不是,请说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)是定值![]() ,理由见解析;
,理由见解析;
【解析】
(Ⅰ)连接AD,由同弧所对的圆周角相等可知∠ACF=∠ADF,由旋转的性质可知AC=AE,利用垂径定理证得AD=AC,推出AE=AD,∠AED=∠ADF,即可推出结论;
(Ⅱ)过点E作EN∥CD,过点D作DN⊥CD,且EN与直线AB交于点M,与直线DN交于点N,先证四边形MNDP是矩形,△EAM≌△ACP,推出MN=PD,MP=ND,EM=AP,AM=CP,再证明△END为等腰直角三角形,推出△EMG为等腰直角三角形,即可通过锐角三角函数推出结论.
解:(Ⅰ)连接![]() ,由同弧所对的圆周角相等可知∠ACF=∠ADF,
,由同弧所对的圆周角相等可知∠ACF=∠ADF,
∵AE是由线段AC绕点A逆时针旋转90°得到,
∴AC=AE,
∵CD⊥AB,
∴AB垂直平分CD,
∴AC=AD,
∴AE=AD,
∴∠AED=∠ADF,
∴∠ACF=∠AED;
(Ⅱ)是定值![]() ,
,
理由:过点E作EN∥CD,过点D作DN⊥CD,且EN与直线AB交于点M,与直线DN交于点N,
∵∠EAC=∠CPA=90°,
∴∠EAM+∠CAB=∠CAB+∠ACP=90°,
∴∠EAM=∠ACP,
∵DN⊥CD,CD⊥AB,
∴DN∥AB,
又∵EN∥CD,
∴四边形MNDP是矩形,
∴∠AME=∠APC=90°,
∵AC=AE,∠EAM=∠ACP,∠AME=∠APC,
∴△EAM≌△ACP,
∴EM=AP,AM=CP,
∵四边形MNDP是矩形,
∴MN=PD,MP=ND,
∵AB是直径,CD⊥AB,
∴MN=PD=CP=AM,
又∵EM=AP,
∴EM+MN=AP+AM,即EN=MP=ND,
∴△END是等腰直角三角形,
∴∠EDN=45°,
∵DN∥AB,
∴∠EGM=∠EDN=45°,
∴△EMG是等腰直角三角形,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
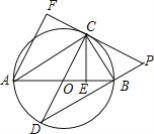
【题目】 如图,AB是⊙O的直径,点E为线段OB上一点(不与O、B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)求证:AC平分∠FAB;
(2)求证:BC2=CECP;
(3)若![]() ,⊙O的面积为12π,求PF的长.
,⊙O的面积为12π,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合采用全面调查(普查)方式的是( )
A.对汀江流域水质情况的调查B.对端午节期间市场上粽子质量情况的调查
C.对某班![]() 名同学身高情况的调查D.对某类烟花爆竹燃放安全情况的调查
名同学身高情况的调查D.对某类烟花爆竹燃放安全情况的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动,如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
(1)填空:BQ=________,PB=________(用含t的代数式表示);
(2)当t为何值时,PQ的长度等于![]() cm?
cm?
(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
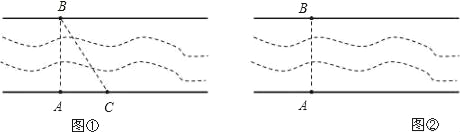
【题目】经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°.
(1)求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);
(2)除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.(不用考虑计算问题,叙述清楚即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB.

(1)求证:AC是⊙O的切线;
(2)若cosC=![]() ,AC=6,求BF的长.
,AC=6,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com