
����Ŀ���ھ���ABCD�У�AB��5 cm��BC��6 cm����P�ӵ�A��ʼ��AB���յ�B��1 cm/s���ٶ��ƶ������ͬʱ����Q�ӵ�B��ʼ�ر�BC���յ�C��2 cm/s���ٶ��ƶ������P��Q�ֱ��A��Bͬʱ����������Q�˶�����Cʱ������ֹͣ�˶������˶�ʱ��Ϊt�룮
(1)��գ�BQ��________��PB��________(�ú�t�Ĵ���ʽ��ʾ)��
(2)��tΪ��ֵʱ��PQ�ij��ȵ���![]() cm?
cm?
(3)�Ƿ����t��ֵ��ʹ�������APQCD���������26 cm2�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�

���𰸡���1��2t cm��(5��t)cm����2����t��3��ʱ��PQ�ij��ȵ���![]() cm����3�����ڣ���t��1��ʱ�������APQCD���������26 cm2�����ɼ�������
cm����3�����ڣ���t��1��ʱ�������APQCD���������26 cm2�����ɼ�������
��������
��1������P��Q������˶��ٶȿɵ�BQ��PB�ij��ȣ�
��2�����ݹ��ɶ����ɵ�PB2+BQ2��QP2��������Ӧ���ݽⷽ�̼��ɣ�
��3����������ɵ���PBQ�����Ϊ������ABCD�������ȥ�����APQCD��������ٸ��������ε������ʽ������Ӧ�߶εij����ɵõ����̣��ٽⷽ�̼��ɣ�
�⣺(1) ��P�ӵ�A��ʼ�ر�AB���յ�B��1cm/s���ٶ��ƶ���
��AP��tcm��
��AB��5cm��
��PB��(5��t)cm��
����Q�ӵ�B��ʼ�ر�BC���յ�C��2cm/s���ٶ��ƶ���
��BQ��2tcm��
�ʴ�Ϊ��2t cm ��(5��t)cm ��
��(2)������ã�(5��t)2��(2t)2��(![]() )2��
)2��
���t1��-1(�������⣬��ȥ)��t2��3��
��t��3��ʱ��PQ�ij��ȵ���![]() cm����
cm����
(3)���ڣ� �������£�
������ABCD������ǣ�5��6��30(cm2)��
ʹ�������APQCD���������26 cm2��
����PBQ�����Ϊ30��26��4(cm2)��
��(5��t) ��2t��![]() ��4��
��4��
���t1��4(�������⣬��ȥ)��t2��1��
����t��1��ʱ��ʹ�������APQCD���������26 cm2��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
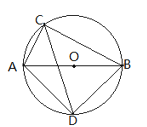
����Ŀ����ͼ����O��ֱ��ABΪ5����ACΪ3����ACB��ƽ���߽���O�ڵ�D��
��1����BC�ij���
��2����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
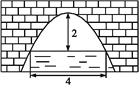
����Ŀ����ͼ��һ�������Ϊ��������״�Ĺ���,��ˮ���4 mʱ,����(���Ŷ�����ߵ�)��ˮ��2 m,��ˮ���½�1 mʱ,ˮ��Ŀ���Ϊ_____m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�У�AB=AC����D��BA���ӳ����ϣ���E��BC�ϣ�DE=DC����F��DE��AC�Ľ��㣬��DF=FE��
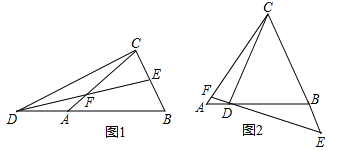
��1��ͼ1���Ƿ��������BDE��ȵĽǣ������ڣ����ҳ���������֤�����������ڣ�˵�����ɣ�
��2����֤��BE=EC��
��3����������D��BA���ӳ����ϣ���E��BC����������F��DE��AC�Ľ��㣬��DF=FE���ֱ��Ϊ����D��AB�ϣ���E��CB���ӳ�������������F��ED���ӳ�����AC�Ľ��㣬��DF=kFE���������������䣨��ͼ2������AB=1����ABC=aʱ����BE�ij����ú�k��a��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ֱ��
ֱ��![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ��ֱ��
��ֱ��![]() ���ֱ�
���ֱ�![]() ��
��![]() ��
��![]() ���㣬����
���㣬����![]() �������߶�
�������߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ���ֱ�
���ֱ�![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��
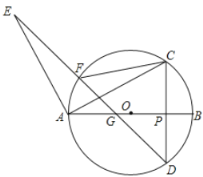
������֤��![]() ��
��
��������![]() ��ֱ��
��ֱ��![]() ���˶��������
���˶��������![]() ��
��![]() �غϣ��������������䣬����
�غϣ��������������䣬����![]() �Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ���˵�����ɣ�
�Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��3000��ѧ����Ϊ�˽�ȫУѧ������ѧ��ʽ����У��ѧ��ȤС�����ʾ��������ʽ����������˸�У����ѧ������Ҫ��ѧ��ʽ(�����ʾ������ѧ��ֻ�ܴ���������������ѡ��һ��)���������������Ƴ����²�������ͳ��ͼ��
���� | A | B | C | D | E | F |
��ѧ��ʽ | �綯�� | ˽�ҳ� | ������ͨ | ���г� | ���� | ���� |
ijУ����ѧ����Ҫ��ѧ��ʽ����ͳ��ͼijУ����ѧ����Ҫ��ѧ��ʽ����ͳ��ͼ

����������Ϣ���ش��������⣺
(1)���뱾���ʾ������ѧ������____�ˣ�����ѡ��B���������____�ˣ�
(2)������ͳ��ͼ�У���E���Ӧ������Բ�Ľ����Ķ���������ȫ����ͳ��ͼ��
(3)����A��C��D��E��������ѧ��ʽ��Ϊ����ɫ������������Ƹ�Уÿ������ɫ��������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y=|a|x2+bx+c��ͼ��A(m,n)��B(0,y1)��C(3��m,n)��D(![]() , y2)��E(2,y3)����y1��y2��y3�Ĵ�С��ϵ��( ).
, y2)��E(2,y3)����y1��y2��y3�Ĵ�С��ϵ��( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
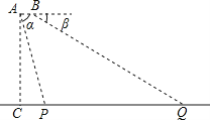
����Ŀ����ͼ��Ϊ�˲���һ�����ŵij��ȣ���һ��ˮƽ���е����˻�AB��β��A������ͷP��ĸ�����=74����ǰ��B������βQ��ĸ���=30������ʱ���˻��ķ��и߶�AC=868�ף�AB=1�ף�����������PQ�ij��ȣ�����������������ο����ݣ�sin74���0.9��cos74���0.3��tan74���3.5��![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������¹涨������ƽ��ֱ������ϵxOy�е�ͼ��M��N���������¶��壺PΪͼ��M������һ�㣬QΪN����һ�㣬���P��Q�����ľ��������Сֵʱ���ͳƸ���СֵΪ����ͼ��M��N֮��ġ��վ��롱�����P��Q�����ľ���������ֵʱ���ͳƸ����ֵΪ����ͼ��M��N֮��ġ������롱��
������ѧϰ��������������Ļ����ϣ�����������⣺
��ƽ��ֱ������ϵxOy�У���A����6��8����B����6����8����C��6����8����D��6��8����
��1������ƽ��ֱ������ϵ�л����ı���ABCD���߶�AB���߶�CD�ġ��վ��롱Ϊ�� �����������롱Ϊ�� ����
��2����ֱ��y����![]() x+b��b��0����x�ᣬy��ֱ��ڵ�E��F�����߶�EF���ı���ABCD�ġ��վ��롱��2�������ǵġ������롱��
x+b��b��0����x�ᣬy��ֱ��ڵ�E��F�����߶�EF���ı���ABCD�ġ��վ��롱��2�������ǵġ������롱��
��3����M��Բ��ΪM��m����6�����뾶Ϊ1������M���ABC�ġ��վ��롱����1��ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com