
【题目】如图,在平面直角坐标系xOy中,将二次函数![]() 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
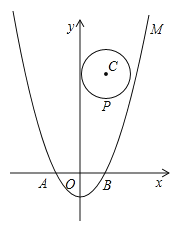
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求![]() 的最大值;
的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)25.
;(3)25.
【解析】
试题分析:(1)根据二次函数N的图象是由二次函数M翻折、平移得到所以a=﹣1,求出二次函数N的顶点坐标即可解决问题.
(2)由![]() =
=![]() 可知OP最大时,
可知OP最大时,![]() 最大,求出OP的最大值即可解决问题.
最大,求出OP的最大值即可解决问题.
(3)画出函数图象即可解决问题.
试题解析:(1)解:二次函数![]() 的图象M沿x轴翻折得到函数的解析式为
的图象M沿x轴翻折得到函数的解析式为![]() ,此时顶点坐标(0,1),将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N的顶点为(2,9),故N的函数表达式
,此时顶点坐标(0,1),将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N的顶点为(2,9),故N的函数表达式![]() ,即
,即![]() .
.
(2)∵A(﹣1,0),B(1,0),∴![]() =
=![]() =
=![]() =
=![]() ,∴当PO最大时
,∴当PO最大时![]() 最大.如图,延长OC与⊙O交于点P,此时OP最大,
最大.如图,延长OC与⊙O交于点P,此时OP最大,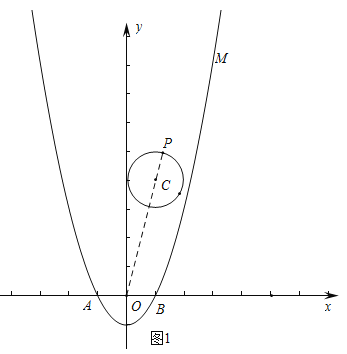
∴OP的最大值=OC+PO=![]() ,∴
,∴![]() 最大值=
最大值=![]() =
=![]() .
.
(3)M与N所围成封闭图形如图所示:

由图象可知,M与N所围成封闭图形内(包括边界)整点的个数为25个.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明在超市买一食品,外包装上印有“总净含量(300±5)g”的字样。小明拿去称了一下,发现只有297g.则食品生产厂家 (填“有”或“没有”)欺诈行为。
查看答案和解析>>
科目:初中数学 来源: 题型:
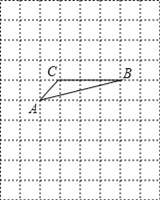
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(Ⅰ)计算AC2+BC2的值等于 ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC2+BC2,并简要说明画图方法(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多项式与3m2 4 的和是m2 m 5 ,则这个多项式为( )
A. 2m2 m 9 B. 2m2 m 1
C. 2m2 m 9 D. 2m2 m 9
查看答案和解析>>
科目:初中数学 来源: 题型:
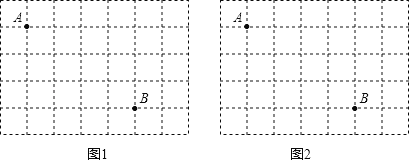
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.
(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.
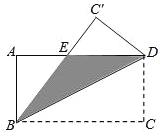
A.72 B.90 C.108 D.144
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com