
【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大
【答案】D
【解析】解:A、∵当a=1,x=﹣1时,y=1+2﹣1=2,∴函数图象不经过点(﹣1,1),故错误;
B、当a=﹣2时,∵△=42﹣4×(﹣2)×(﹣1)=8>0,∴函数图象与x轴有两个交点,故错误;
C、∵抛物线的对称轴为直线x=﹣ ![]() =1,∴若a>0,则当x≥1时,y随x的增大而增大,故错误;
=1,∴若a>0,则当x≥1时,y随x的增大而增大,故错误;
D、∵抛物线的对称轴为直线x=﹣ ![]() =1,∴若a<0,则当x≤1时,y随x的增大而增大,故正确;
=1,∴若a<0,则当x≤1时,y随x的增大而增大,故正确;
所以答案是:D.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在过去的学习中已经发现了如下的运算规律:
(1)15×15=1×2×100+25=225;
(2)25×25=2×3×100+25=625;
(3)35×35=3×4×100+25=1225;
……
按照这种规律,第n个式子可以表示为
A. n×n=![]() ×(
×(![]() +1)×100+25=n2
+1)×100+25=n2
B. n×n=![]() ×(
×(![]() +1)×100+25=n2
+1)×100+25=n2
C. (n+5)×(n+5)=n×(n+1)×100+25=n2+10n+25
D. (10n+5)×(10n+5)=n×(n+l)×l00+25=100n2+100n+25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.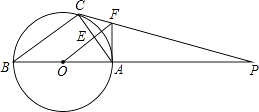
(1)判断AF与⊙O的位置关系并说明理由;
(2)已知半径为20,AF=15,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
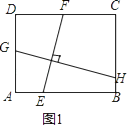
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() =
= ![]() ;
;
(2)【结论应用】如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 ![]() =
= ![]() ,则
,则 ![]() 的值为;
的值为;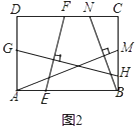
(3)【联系拓展】如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 ![]() 的值.
的值.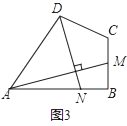
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在公园道一号购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:

(1)用含x的代数式表示地面总面积
(2)当x=3时,若铺1m2地砖的平均费用为100元, 那么王老师要将全部地面铺地砖,总费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com