练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于x的一元二次方程x2－2x－m2＝0．

    （1）求证：该方程有两个不相等的实数根；

    （2）若该方程有两个实数根为x1，x2，且x1＝2x2＋5，求m的值．

    【答案】（1）证明见解析；（2）

    【解析】试题分析:(1)先计算判别式的值,然后根据整式的性质判断与0的关系,即可求证,

    (2)根据一元二次方程根与系数关系可得: ,,由可得: ,所以,解得: ,再根据,可得:

    ,即可求解m.

    试题解析:（1）证明:∵b2－4ac＝(－2)2－4(－m2)＝4＋4m2,

    ∵≥0,

    ∴4＋4m2＞0,

    ∴b2－4ac＞0,

    ∴该方程有两个不相等的实数根,

    （2）由题意，得x1＋x2＝2，x1x2＝ －m2,

    又∵x1＝2x2＋5,

    ∴x1＝3,x2＝－1,

    ∴－m2＝－3,即m2＝3,

    解得m＝.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】国家规定个人发表文章、出版图书获得稿费的纳税计算方法是：(l)稿费不高于800元的不纳税；(2)稿费高于800元又不高于4000元的，减除其中的800元，其余部分按20%纳税：(3)稿费高于4000元，减除稿酬的20%，其余部分按20%纳税.今知丁老师获得一笔稿费，并缴纳个人所得税600元，问：丁老师的这笔稿费有多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0（a≠0）的求根公式时，对于b2﹣4ac＞0的情况，她是这样做的：

    由于a≠0，方程ax2+bx+c=0变形为：

    x2+x=﹣，…第一步

    x2+x+（）2=﹣+（）2，…第二步

    （x+）2=，…第三步

    x+=（b2﹣4ac＞0），…第四步

    x=，…第五步

    嘉淇的解法从第　　步开始出现错误；事实上，当b2﹣4ac＞0时，方程ax2+bx+c=0（a≠O）的求根公式是　　．

    用配方法解方程：x2﹣2x﹣24=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】反比例函数在第一象限的图象如图所示，过点A（1，0）作x轴的垂线，交反比例函数的图象于点M，△AOM的面积为3．

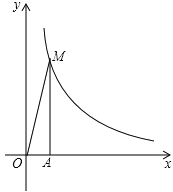
    （1）求反比例函数的解析式；

    （2）设点B的坐标为（t，0），其中t＞1．若以AB为一边的正方形有一个顶点在反比例函数的图象上，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．

    （1）证明：AF=CE；

    （2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．

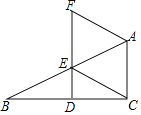
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的口袋中装有2个红球（记为红1、红2），1个白球、1个黑球，这些球除颜色外都相同，将球搅匀．

    （1）从中任意摸出1个球，恰好摸到红球的概率是 ；

    （2）先从中任意摸出一个球，再从余下的3个球中任意摸出1个球，请用画树状图或列表法求两次都摸到红球的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班学生参加公民道德知识竞赛，将竞赛所取得的成绩（得分取整数）进行整理后分成5组，并绘制成频率分布直方图，如下图所示，请结合直方图提供的信息，回答下列问题．

    （1）该班共有多少名学生？

    （2）60.5～70.5这一分数段的频数、频率分别是多少？

    （3）根据统计图，提出一个问题，并回答你所提出的问题？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的，∠BAC=90°，AB=6，AC=8，点D，E，F，G，H，I都在长方形KLMJ的边上，则长方形KLMJ的面积为（

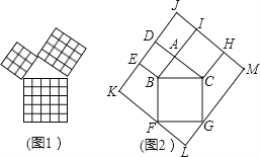
    A. 360 B. 400 C. 440 D. 484

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当m是何值时，关于x的方程（m2+2）x2+（m﹣1）x﹣4=3x2

    （1）是一元二次方程；

    （2）是一元一次方程；

    （3）若x=﹣2是它的一个根，求m的值．

    查看答案和解析>>

    同步练习册答案