
【题目】某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
另一部分鲜花在淘宝网销售,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 关系如下图所示.

(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;
(2)观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;
(3)设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值.
【答案】(1)![]() (0≤x≤20);(2)销售8天后,该花木公司采用了降价促销(或广告宣传)的方法吸引了淘宝买家的注意力,日销量逐渐增加.
(0≤x≤20);(2)销售8天后,该花木公司采用了降价促销(或广告宣传)的方法吸引了淘宝买家的注意力,日销量逐渐增加. ;(3)第12天,日销售总量最大,最大值为32万朵.
;(3)第12天,日销售总量最大,最大值为32万朵.
【解析】
试题(1)由图表数据观察可知y1与x之间是二次函数关系,设![]() 将(4,16)代入即可求得结果;
将(4,16)代入即可求得结果;
(2)仔细分析图象特征结合待定系数法求函数关系式进行求解即可;
(3)先求出y关于x的二次函数,再根据二次函数的性质求解即可.
(1)由图表数据观察可知y1与x之间是二次函数关系,
设![]() 将(4,16)代入得:
将(4,16)代入得:![]()
∴y1与x函数关系式为![]() (0≤x≤20);
(0≤x≤20);
(2)销售8天后,该花木公司采用了降价促销(或广告宣传)的方法吸引了淘宝买家的注意力,日销量逐渐增加, ;
;
(3)当0≤x≤8时,![]()
![]()
![]()
![]()
∵抛物线开口向下,x的取值范围在对称轴左侧,y随x的增大而增大,
∴当x=8时y有最大值为28
当8<x≤20时,![]()
![]()
![]()
![]()
∵抛物线开口向下,顶点在x的取值范围内
∴当x=12时y有最大值为32
∴该花木公司销售第12天,日销售总量最大,最大值为32万朵.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记∠AMP=![]() ,∠ONQ=
,∠ONQ=![]() ,当MP+PQ+QN最小时,则
,当MP+PQ+QN最小时,则![]() 与
与![]() 的数量关系是_________________.
的数量关系是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M的左侧).
(1)当BM的长为10时,求证:BD⊥DM;
(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;
(3)如果△DMN是等腰三角形,求BN的长.
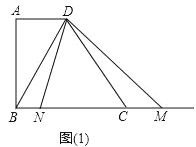

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象经过点A(0,4)和点B(3,0),以线段AB为边在第一象限内作等腰直角△ABC,使∠BAC=90°.

(1)求一次函数的解析式;
(2)求出点C的坐标;
(3)点P是y轴上一动点,当PB+PC最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等.
(1)甲、乙二人每小时各做零件多少个?
(2)甲做几小时与乙做4小时所做机械零件数相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的动点,M为线段EF上一动点,则BM+DM最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() .
.![]() 、
、![]() 是边
是边![]() 、
、![]() 边上的动点,
边上的动点,![]() 从
从![]() 出发向
出发向![]() 运动,同时
运动,同时![]() 以相同的速度从
以相同的速度从![]() 出发向
出发向![]() 运动,
运动,![]() 运动到
运动到![]() 停止.
停止.![]() 为
为![]() 中点.
中点.
![]() 试探究
试探究![]() 的形状,并说明理由.
的形状,并说明理由.
![]() 在运动过程中,四边形
在运动过程中,四边形![]() 可能成为正方形吗?如能求正方形的边长.
可能成为正方形吗?如能求正方形的边长.
![]() 当
当![]() 为多少时,
为多少时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ACB=90°,AC=BC,点D在斜边AB上,且AD=AC,过点B作BE⊥CD交CD的延长线于点E.
(1)画出符合题意的图形;
(2)求∠BCD的度数;
(3)求证:CD=2BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com