
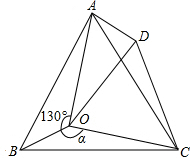
 如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.| 2 |
| 3 |
| 2 |
| 3 |


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
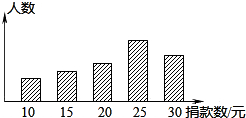 为支持我国西南地区抗旱救灾,团中央和全国少工委号召全国各级共青团和少先队组织,积极组织动员广大共青团员和少先队员,每人捐助一瓶水,用实际行动向灾区人民群众送去“爱心水”. 某校对本校倡导的自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人.请你根据上述信息解答下列问题:
为支持我国西南地区抗旱救灾,团中央和全国少工委号召全国各级共青团和少先队组织,积极组织动员广大共青团员和少先队员,每人捐助一瓶水,用实际行动向灾区人民群众送去“爱心水”. 某校对本校倡导的自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人.请你根据上述信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
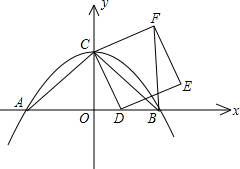 已知抛物线y=-
已知抛物线y=-| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
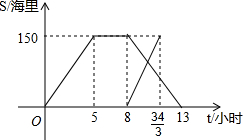 一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com