Question

【题目】如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，且AF=DF．

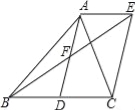
（1）求证：四边形ADCE是平行四边形；

（2）当AB、AC之间满足 时，四边形ADCE是矩形；

（3）当AB、AC之间满足 时，四边形ADCE是正方形．

Answer 1

【答案】（1）证明见解析（2）当AB=AC时（3）当AB=AC，AB⊥AC时

【解析】

试题分析：（1）首先证明△AFE≌△DFB可得AE=BD，进而可证明AE=CD，再由AE∥BC可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形；

（2）当AB=AC时，根据等腰三角形三线合一可得AD⊥BC，再根据有一个角是直角的平行四边形是矩形可得结论；

（3）当AB=AC，AB⊥AC时，△ABC是等腰直角三角形，根据直角三角形斜边上的中线等于斜边的一半可得AD=CD，根据等腰三角形的性质可得AD⊥BC，从而可得证明四边形ADCE是正方形．

试题解析： （1）∵AD是△ABC的中线，

∴BD=CD，

∵AE∥BC，

∴∠AEF=∠DBF，

在△AFE和△DFB中，

，

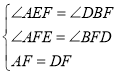∴△AFE≌△DFB（AAS），

∴AE=BD，

∴AE=CD，

∵AE∥BC，

∴四边形ADCE是平行四边形；

（2）当AB=AC时，四边形ADCE是矩形；

∵AB=AC，AD是△ABC的中线，

∴AD⊥BC，

∴∠ADC=90°，

∵四边形ADCE是平行四边形，

∴四边形ADCE是矩形，

故答案为：AB=AC；

（3）当AB⊥AC，AB=AC时，四边形ADCE是正方形，

∵AB⊥AC，AB=AC，

∴△ABC是等腰直角三角形，

∵AD是△ABC的中线，

∴AD=CD，AD⊥BC，

又∵四边形ADCE是平行四边形，

∴四边形ADCE是正方形，

故答案为：AB⊥AC，AB=AC．