
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E

(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB=![]() ,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
试题解析:(1)∵四边形ABCD是矩形,∴∠B=90°,AD=BC,AD∥BC,∴∠DAE=∠AFB,∵DE⊥AF,∴∠AED=90°=∠B,在△ABF和△DEA中,∵∠AFB=∠DAE,∠B=∠DEA,AF=AD,∴△ABF≌△DEA(AAS),∴DE=AB;
(2)∵BC=AD,AD=AF,∴BC=AF,∵BF=1,∠ABF=90°,∴由勾股定理得:AB=![]() =
=![]() ,∴∠BAF=30°,∵△ABF≌△DEA,∴∠GDE=∠BAF=30°,DE=AB=DG=
,∴∠BAF=30°,∵△ABF≌△DEA,∴∠GDE=∠BAF=30°,DE=AB=DG=![]() ,∴扇形ABG的面积=
,∴扇形ABG的面积=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将边为![]() 的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
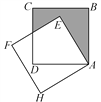
A. ![]() -
-![]() B. 3-
B. 3-![]() C. 2-
C. 2-![]() D. 2-
D. 2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去租用这两种货车情况如下:
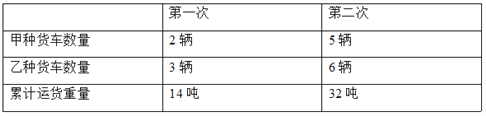
(1)分别求甲、乙两种货车载重多少吨?
(2)现在租用该公司5辆甲货车和7辆乙货车一次刚好运完这批货物,如果按每吨付费50元计算,货主应付运费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
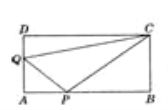
【题目】如图,在矩形AB CD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动;点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0<t<6).
(1)当t为何值时,△QAP为等腰直角三角形?
(2)四边形QAPC的面积与t的大小有关系吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
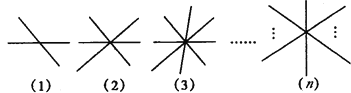
【题目】(1)两条直线相交于一点有2组不同的对顶角;
(2)三条直线相交于一点有6组不同的对顶角;
(3)四条直线相交于一点有12组不同的对顶角;
(4)n条直线相交于同一点有___________组不同对顶角.(如图所示)
查看答案和解析>>
科目:初中数学 来源: 题型:
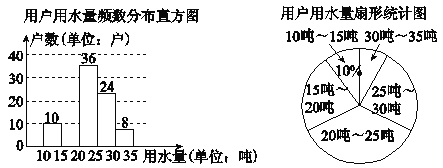
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
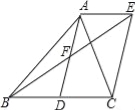
(1)求证:四边形ADCE是平行四边形;
(2)当AB、AC之间满足 时,四边形ADCE是矩形;
(3)当AB、AC之间满足 时,四边形ADCE是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com