练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】a+b=5，ab=2，则（a﹣2）（3b﹣6）= ．

    【答案】-12
    【解析】解：∵a+b=5，ab=2， ∴（a﹣2）（3b﹣6）
    =3ab﹣6a﹣6b+12
    =3ab﹣6（a+b）+12
    =3×2﹣6×5+12
    =﹣12．
    所以答案是：﹣12．
    【考点精析】本题主要考查了多项式乘多项式的相关知识点，需要掌握多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料解决问题：

    材料：古希腊著名数学家 毕达哥拉斯发现把数1，3，6，10，15，21…这些数量的（石子），都可以排成三角形，则称像这样的数为三角形数．

    把数 1，3，6，10，15，21…换一种方式排列，即

    1=1

    1+2=3

    1+2+3=6

    1+2+3+4=10

    1+2+3+4+5=15

    …

    从上面的排列方式看，把1，3，6，10，15，…叫做三角形数“名副其实”．

    （1）设第一个三角形数为a1=1，第二个三角形数为a2=3，第三个三角形数为a3=6，请直接写出第n个三角形数为an的表达式（其中n为正整数）．

    （2）根据（1）的结论判断66是三角形数吗？若是请说出66是第几个三角形数？若不是请说明理由．

    （3）根据（1）的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在某一平地上，有一棵树高8米的大树，一棵树高3米的小树，两树之间相距12米。今一只小鸟在其中一棵树的树梢上，要飞到另一棵树的树梢上，问它飞行的最短距离是多少？（画出草图然后解答）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式中，计算正确的是（　　）

    A. （a﹣b）2=a2﹣b2 B. （2x﹣y）2=4x2﹣2xy+y2

    C. (a﹣3b）（a+3b）=a2﹣9b2 D. (15 x2 y-10x y2) ÷5xy=3x-2 y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△AOB和Rt△COD中，∠AOB=∠COD=90°，∠B=50°，∠C=60°，点D在边OA上，将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周，在旋转的过程中，在第t秒时，边CD恰好与边AB平行，则t的值为 ．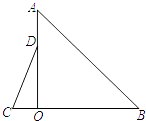

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据4，1，7，4，5，6则这组数据的极差为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列图形中，既是轴对称图形又是中心对称图形的是（　　）

    A.等边三角形B.菱形C.平行四边形D.正五边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．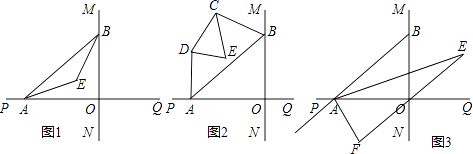
    （1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A，B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
    （2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A，B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．
    （3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E，F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角平分线CF于点F．

    （1）求证：AE=EF；

    （2）如图2，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，（1）中的结论是否仍然成立？　　；（填“成立”或“不成立”）；

    （3）如图3，若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”，其余条件仍不变，那么结论AE=EF是否成立呢？若成立请证明，若不成立说明理由．

    查看答案和解析>>

    同步练习册答案