
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.

(1)求证:AE=EF;
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,(1)中的结论是否仍然成立? ;(填“成立”或“不成立”);
(3)如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请证明,若不成立说明理由.
【答案】(1)证明见解析;(2)成立;(3)成立,证明见解析.
【解析】试题分析:(1)取AB中点M,连接EM,求出BM=BE,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(2)截取BE=BM,连接EM,求出AM=EC,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(3)在BA的延长线上取一点N,使AN=CE,连接NE,根据已知利用ASA判定△ANE≌△ECF,因为全等三角形的对应边相等,所以AE=EF.
试题解析:(1)证明:取AB中点M,连接EM,
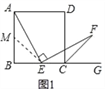
∵AB=BC,E为BC中点,M为AB中点,
∴AM=CE=BE,
∴∠BME=∠BME=45°,
∴∠AME=135°=∠ECF,
∵∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
在△AME和△ECF中, 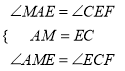
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)成立,
理由是:如图,在AB上截取BM=BE,连接ME,
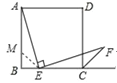
∵∠B=90°,
∴∠BME=∠BEM=45°,
∴∠AME=135°=∠ECF,
∵AB=BC,BM=BE,
∴AM=EC,
在△AME和△ECF中, 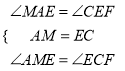
∴△AME≌△ECF(ASA),
∴AE=EF;
(3)成立.
证明:如图,在BA的延长线上取一点N.使AN=CE,连接NE,
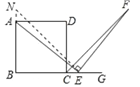
∴BN=BE,
∴∠N=∠NEC=45°,
∵CF平分∠DCG,
∴∠FCE=45°,
∴∠N=∠ECF,
∵四边形ABCD是正方形,
∴AD∥BE,
∴∠DAE=∠BEA,即∠DAE+90°=∠BEA+90°,
∴∠NAE=∠CEF,
∴△ANE≌△ECF(ASA),
∴AE=EF.


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°. 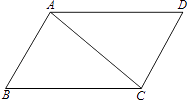
(1)试说明AD∥BC.
(2)若AB与CD也平行,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益Z(元)会相应降低且Z与x之间也大致满足如图②所示的一次函数关系。

(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,每瓶进价为4元.经市场调查表明,当售价在5元到8元之间(含5元,8元)浮动时,每瓶售价每增加1元,日均销售量减少40瓶;当售价为每瓶为6元时,日均销售量为120瓶.问:销售价格定为每瓶多少元时,所得日均毛利润(每瓶毛利润=每瓶售价-每瓶进价)最大?最大日均毛利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象的对称轴是直线x=2,且图象过点(1,2),与一次函数y=x+m的图象交于(0,-1).
求两个函数解析式;
求两个函数图象的另一个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF、CF.

(1)如图1, 当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com