
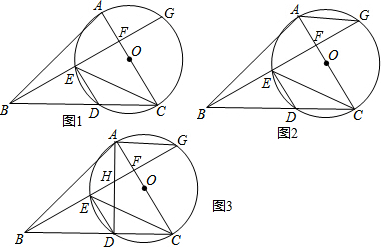
分析 (1)根据自变量与函数值的对应关系,可得A、B点坐标,再把A、B两点坐标代入y=ax2-6ax+c,利用待定系数法,可得抛物线的解析式;
(2)设抛物线对称轴交x轴于点F,作DE⊥CF于点E.利用AAS证明△ACF≌△CDE,根据全等三角形的性质,可得AF=CE,CF=DE,设C(3,m),则AF=CE=4,CF=DE=m,D(m+3,m-4),将D(m+3,m-4)代入抛物线的解析式,可得关于m的方程,解方程,可得答案;
(3)先求出∠AGF=∠DGE=45°,则∠AGD=90°,∠MCN=$\frac{1}{2}$∠AGD=45°.在BA延长线上取一点H,使AH=DN,证明△ACH≌△DCN,得出CH=CN,∠HCA=∠NCD,再证明△MCH≌△MCN,得出∠HMC=∠NMC.作CK⊥HM于K,求出CG=7,解Rt△CKG,得出CK=CG•sin∠CGK=$\frac{7}{2}$$\sqrt{2}$,则CP=$\frac{7}{2}$$\sqrt{2}$,t=3-$\frac{7}{2}$$\sqrt{2}$.
解答 解:(1)直线y=-x-1与坐标轴交点坐标A(-1,0),B(0,-1).
∵抛物线y=ax2-6ax+c经过A、B两点,
∴$\left\{\begin{array}{l}{(-1)^{2}a-6a×(-1)+c=0}\\{c=-1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=\frac{1}{7}}\\{c=-1}\end{array}\right.$,
∴y=$\frac{1}{7}$x2-$\frac{6}{7}$x-1;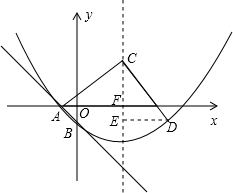 (2)如图,设抛物线对称轴交x轴于点F,作DE⊥CF于点E,
(2)如图,设抛物线对称轴交x轴于点F,作DE⊥CF于点E,
∵y=$\frac{1}{7}$x2-$\frac{6}{7}$x-1的对称轴x=3,
∴F(3,0).
∵CF⊥x轴,DE⊥CE,
∴∠AFC=∠AFE=∠CED=90°.
∵∠CAF+∠ACF=∠DCE+∠ACF=90°,
∴∠CAF=∠DCE.
在△ACF和△CDE中,
$\left\{\begin{array}{l}{∠CAF=∠DCE}\\{∠AFC=∠CED=90°}\\{AC=CD}\end{array}\right.$,
∴△ACF≌△CDE(AAS),
∴AF=CE,CF=DE.
设C(3,m),则AF=CE=4,CF=DE=m,D(m+3,m-4),
将D(m+3,m-4)代入抛物线的解析式,
得m-4=$\frac{1}{7}$(m+3)2-$\frac{6}{7}$(m+3)-1,
解得m1=3,m2=4(舍),
∴D(6,-1);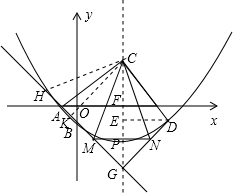 (3)由(1)知A(-1,0),由(2)知F(3,0),
(3)由(1)知A(-1,0),由(2)知F(3,0),
则OA=1,OF=3.
∴AF=4.
由(2)知DE=3,C(3,3),
当x=3时,y=-3-1=-4,
∴G(3,-4),
∴AF=FG=4,
∵D(6,-1),
∴EF=1,
∴EG=3.
∴DE=GE=3,
∵∠AFG=∠DEG=90°,
∴∠FAG=∠FGA=45°,∠EDG=∠EGD=45°,
∴∠AGF=∠DGE=45°,
∴∠AGD=90°.
∵∠MCN=$\frac{1}{2}$∠AGD,
∴∠MCN=45°.
在四边形CAGD中,∵∠CAG+∠AGD+∠CDG+∠ACD=360°,
∴∠CAG+∠CDG=180°.
如图,在BA延长线上取一点H,使AH=DN,
∵∠CAG+∠CAH=180°,
∴∠CAH=∠CDG.
∵AC=CD,
∴△ACH≌△DCN,
∴CH=CN,∠HCA=∠NCD.
∵∠ACN+∠NCD=90°,
∴∠ACN+∠HCA=90°,
∴∠HCM=∠NCM=45°.
在△MCH与△MCN中,
$\left\{\begin{array}{l}{CH=CN}\\{∠HCM=∠NCM}\\{CM=CM}\end{array}\right.$,
∴△MCH≌△MCN,
∴∠HMC=∠NMC.
∵MN∥x轴,
∴CP⊥MN,
作CK⊥HM于K,
∴CK=CP,由C(3,3),G(3,-4),
∴CG=7.
在Rt△CKG中,CK=CG•sin∠CGK=$\frac{7}{2}$$\sqrt{2}$,
∴CP=$\frac{7}{2}$$\sqrt{2}$,
∴t=3-$\frac{7}{2}$$\sqrt{2}$.
点评 本题是二次函数综合题,其中涉及到待定系数法求二次函数解析式、旋转的性质、全等三角形的判定与性质、函数图象上点的坐标特征等知识.本题综合性较强,难度较大,准确作出辅助线利用数形结合是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
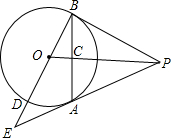 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
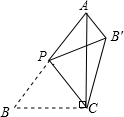 如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:
如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com