
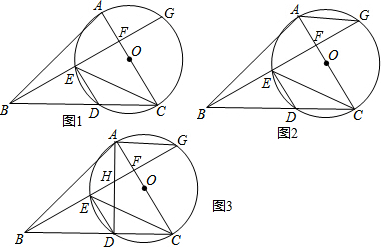
分析 (1)连接AD,由AC是⊙O的直径知∠DAC+∠ACD=90°,又由∠DEC=∠DAC=∠EBC可得∠EBC+∠ACD=90°,即∠BFC=90°;
(2)连接AD、GC,由AC是⊙O的直径可得∠ADC=∠AGC=90°,根据AG∥BC证得四边形GADC是矩形,故AG=DC;
(3)根据FH:HE=1:2,可设FH=a、HE=2a,由∠BFC=90°知FG=FE=3a且∠HAF+∠AHF=90°,又由∠HAF+∠FAG=90°可得∠AHF=∠FAG,则有$\frac{AF}{HF}=\frac{FG}{AF}$,根据比例式求得a的值,进而知HF=1、EH=2、FG=3、GH=4,由∠ACE=∠AGE=∠EBC=∠DEC得∠DEC=∠ACE,故DE∥AC,即$\frac{AH}{DH}=\frac{HF}{HE}$,又由$\frac{AH}{DH}=\frac{GH}{BH}$,可得$\frac{GH}{BH}=\frac{HF}{HE}=\frac{1}{2}$,据此可得HB的长即可.
解答 解:(1)如图1,连接AD,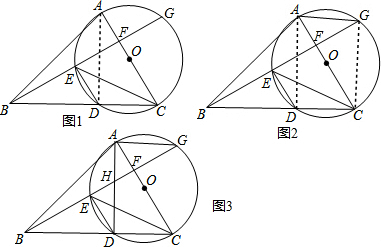
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠ACD=90°,
∵$\widehat{DC}=\widehat{DC}$,
∴∠DEC=∠DAC,
又∵∠DEC=∠EBC,
∴∠DAC=∠EBC,
∴∠EBC+∠ACD=90°,
∴∠BFC=90°;
(2)如图2,连接AD、GC,
∵AC是⊙O的直径,
∴∠ADC=∠AGC=90°,
∵AG∥BC,
∴∠GAD+∠ADC=180°,
∴∠GAD=90°,即∠GAD=∠ADC=∠CGA=90°,
∴四边形GADC是矩形,
∴AG=DC;
(3)∵FH:HE=1:2,
∴设FH=a(a>0),则HE=2a,
由(1)知∠BFC=90°,
∴OF⊥EG于点F,∠HAF+∠AHF=90°,
∴FG=FE=3a,
由(2)知∠HAF+∠FAG=90°,
∴∠AHF=∠FAG,
∴tan∠AHF=tan∠FAG,
∴$\frac{AF}{HF}=\frac{FG}{AF}$,
∴AF2=HF•FG,
∴($\sqrt{3}$)2=a•3a,
∴3a2=3,
∵a>0,
∴a=1,
∴HF=1,EH=2,FG=3,
∴GH=4,
∵$\widehat{AE}=\widehat{AE}$,
∴∠ACE=∠AGE,
∵AG∥BC,
∴∠AGE=∠EBC,
又∵∠EBC=∠DEC,
∴∠DEC=∠ACE,
∴DE∥AC,
∴$\frac{AH}{DH}=\frac{HF}{HE}$,
∵AG∥BC,
又∵GH=4,
∴HB=8,
∴BE=BH-HE=8-2=6.
点评 本题考查的是垂径定理、圆周角定理、线段的比等知识点,根据角与角间的转换得出线段平行,从而根据平行得到线段的比求出长度是关键.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
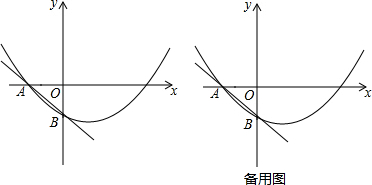
 如图,在平面直角坐标系中,所有小方格的边长都为1个单位长度.
如图,在平面直角坐标系中,所有小方格的边长都为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
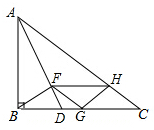 Rt△ABC,∠ABC=90°,AD平分∠BAC,BF⊥AC交AD于F,FH∥BC交于H,FG∥AC
Rt△ABC,∠ABC=90°,AD平分∠BAC,BF⊥AC交AD于F,FH∥BC交于H,FG∥AC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
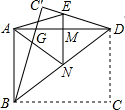 如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于M,则ME=$\frac{7}{12}$.
如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于M,则ME=$\frac{7}{12}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com