
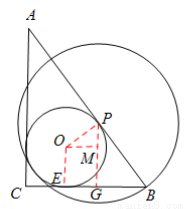
如图,在Rt△ABC中,∠ACB=90°,AC=4 cm ,BC=3 cm,⊙O为△ABC的内切圆.
(1)求⊙O的半径;
(2)点P从点B沿边BA向点A以点1cm/s 的速度匀速运动,以点P为圆心,PB长为半径作圆.设点P运动的时间为 t s.若⊙P与⊙O相切,求t的值.

(1)1 cm;(2)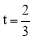 或2.
或2.
【解析】
试题分析:(1)设⊙O与AB,BC,CA的切点分别为D,E,F,连接OD,OE,OF,根据切线的性质证明四边形CEOF是正方形,由勾股定理求AB的长,把AD,BD用半径r的代数式表示,从而根据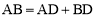 列方程求解即可.
列方程求解即可.
(2)为⊙P与⊙O外切和⊙P与⊙O内切两种情况讨论即可.
试题解析:(1)如图,设⊙O与AB,BC,CA的切点分别为D,E,F,连接OD,OE,OF,
则AD=AF,BD=BE,CE=CF.
∵⊙O为△ABC的内切圆,∴OF⊥AC,OE⊥BC,即∠OFC=∠OEC=90°.
又∵∠C=90°,∴四边形CEOF是矩形.
又∵OE=OF,∴四边形CEOF是正方形.
设⊙O的半径为r cm,则FC=EC=OE= r cm,
在Rt△ABC中,∠ACB=90°,AC=4 cm ,BC=3 cm,∴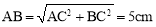 .
.
∵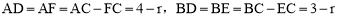 ,
,
∴ ,解得r=1.
,解得r=1.
∴⊙O的半径为1 cm.
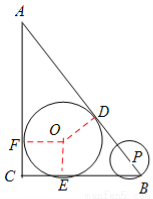
(2)如图,过点P作PG⊥BC于点G,
∵∠PGB=∠C=90°,∴PG∥AC.∴△PBG∽△ABC.∴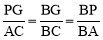 .
.
又∵BP=t,∴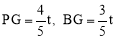 .
.
若⊙P与⊙O相切,,则可分为⊙P与⊙O外切和⊙P与⊙O内切两种情况:
①如图,当⊙P与⊙O外切时,连接OP,则OP=1+t.
过点P作PH⊥OE于点H,
∵∠PHE=∠HEG=∠PGE=90°,∴四边形PHEG是矩形.∴HE=PG,PH=GE.
∴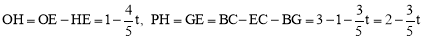 .
.
在Rt△OPH中,由勾股定理,得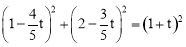 ,解得
,解得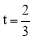 .
.
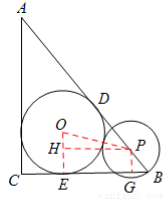
②如图,当⊙P与⊙O内切时,连接OP,则OP=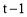 .
.
过点O作OM⊥PG于点M,
∵∠MGE=∠OEG=∠OMG=90°,∴四边形OEGM是矩形.∴MG=OE,OM=EG.
∴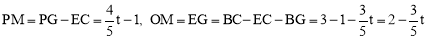 .
.
在Rt△OPM中,由勾股定理,得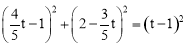 ,解得
,解得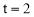 .
.
综上所述,当⊙P与⊙O相切时,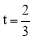 或2.
或2.
考点:1.单动点和面动问题;2.直线与圆相切的性质;3.矩形、正方形的判定和性质;4.勾股定理;5.相似三角形的判定和性质;6.方程思想和分类思想的应用.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源:2014年初中毕业升学考试(江苏徐州卷)数学(解析版) 题型:填空题
在平面直角坐标系中,将点A(4,2)绕原点逆时针方向旋转90°后,其对应点A′的坐标为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:填空题
某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是 分.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
为了了解某市120000名初中学生的视力情况,某校数学兴趣小组,并进行整理分析.
(1)小明在眼镜店调查了1000名初中学生的视力,小刚在邻居中调查了20名初中学生的视力,他们的抽样是否合理?并说明理由.
(2)该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.
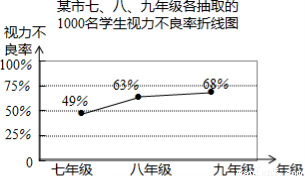
请你根据抽样调查的结果,估计该市120000名初中学生视力不良的人数是多少?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:填空题
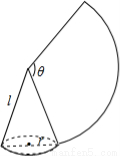
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面圆半径r=2cm,扇形圆心角 ,则该圆锥母线长l为 cm.
,则该圆锥母线长l为 cm.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:解答题
马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:选择题
某班第一组12名同学在“爱心捐款”活动中,捐款情况统计如下表,则捐款数组成的一组数据中,中位数与众数分别是( )
捐款(元) | 10 | 15 | 20 | 50 |
人数 | 1 | 5 | 4 | 2 |
A.15,15 B.17.5,15 C.20,20 D.15,20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com