
【题目】为了落实党的“精准扶贫”政策,![]() 、
、![]() 两城决定向
两城决定向![]() 、
、![]() 两乡运送肥料以支持农村生产,已知
两乡运送肥料以支持农村生产,已知![]() 、
、![]() 两城共有肥料
两城共有肥料![]() 吨,其中
吨,其中![]() 城肥料比
城肥料比![]() 城少
城少![]() 吨,从
吨,从![]() 城往
城往![]() 、
、![]() 两乡运肥料的费用分别为
两乡运肥料的费用分别为![]() 元/吨和
元/吨和![]() 元/吨,从
元/吨,从![]() 城往
城往![]() 、
、![]() 两乡运肥料的费用分别为
两乡运肥料的费用分别为![]() 元/吨和
元/吨和![]() 元/吨,现
元/吨,现![]() 乡需要肥料
乡需要肥料![]() 吨,
吨,![]() 乡需要肥料
乡需要肥料![]() 吨.
吨.
(1)![]() 城和
城和![]() 城各有多少吨肥料?
城各有多少吨肥料?
(2)设从![]() 城运往
城运往![]() 乡肥料
乡肥料![]() 吨,总运费为
吨,总运费为![]() 元,求处最少总运费;
元,求处最少总运费;
(3)由于更换车型,使![]() 城运往
城运往![]() 乡的运费每吨减少
乡的运费每吨减少![]()
![]() 元,这时怎样调运才能使总运费最少?
元,这时怎样调运才能使总运费最少?
【答案】(1)A城和B城分别有200吨和300吨肥料;(2)10040元;(3)当![]() 时,A城肥料全部运往D乡,BB城运往C城240吨,运往
时,A城肥料全部运往D乡,BB城运往C城240吨,运往![]() 乡60吨,运费最少;当
乡60吨,运费最少;当![]() 时,不管
时,不管![]() 城肥料运往
城肥料运往![]() 乡多少吨,运费都是10040元;当
乡多少吨,运费都是10040元;当![]() 时,
时,![]() 城肥料全部运往
城肥料全部运往![]() 乡,
乡,![]() 城运往
城运往![]() 城40吨,运往
城40吨,运往![]() 乡260吨,运费最少
乡260吨,运费最少
【解析】
(1)设![]() 城有肥料
城有肥料![]() 吨,
吨,![]() 城有肥料
城有肥料![]() 吨,根据“
吨,根据“![]() 、
、![]() 两城共有肥料
两城共有肥料![]() 吨”和“
吨”和“![]() 城肥料比
城肥料比![]() 城少
城少![]() 吨”两个等量关系式列出方程组求解即可;
吨”两个等量关系式列出方程组求解即可;
(2)设从![]() 城运往
城运往![]() 乡肥料
乡肥料![]() 吨,则从
吨,则从![]() 城运往
城运往![]() 乡
乡![]() 吨,从
吨,从![]() 城运往
城运往![]() 乡肥料
乡肥料![]() 吨,则从
吨,则从![]() 城运往
城运往![]() 乡
乡![]() 吨,若总运费为
吨,若总运费为![]() 元,根据等量关系列出函关系式求解即可;
元,根据等量关系列出函关系式求解即可;
(3)从![]() 城运往
城运往![]() 乡肥料
乡肥料![]() 吨,由于
吨,由于![]() 城运往
城运往![]() 乡的运费每吨减少
乡的运费每吨减少![]() 元可得
元可得![]()
![]() ,然后分三种情况进行讨论即可.
,然后分三种情况进行讨论即可.
解:(1)设![]() 城有肥料
城有肥料![]() 吨,
吨,![]() 城有肥料
城有肥料![]() 吨
吨
根据题意,得![]()
解得![]()
∴A城和B城分别有200吨和300吨肥料;
(2)设从![]() 城运往
城运往![]() 乡肥料
乡肥料![]() 吨,则从
吨,则从![]() 城运往
城运往![]() 乡
乡![]() 吨,从
吨,从![]() 城运往
城运往![]() 乡肥料
乡肥料![]() 吨,则从
吨,则从![]() 城运往
城运往![]() 乡
乡![]() 吨,若总运费为
吨,若总运费为![]() 元,根据题意,得:
元,根据题意,得:
![]()
![]()
由于![]() 是一次函数,
是一次函数,![]() ,
,
![]() 随
随![]() 的增大而增大.
的增大而增大.
![]() ,
,
∴当![]() 时,运费最少,最少运费是10040元.
时,运费最少,最少运费是10040元.
(3)从![]() 城运往
城运往![]() 乡肥料
乡肥料![]() 吨,由于
吨,由于![]() 城运往
城运往![]() 乡的运费每吨减少
乡的运费每吨减少![]() 元
元
![]()
![]()
①当![]() 时,
时,![]()
∴当![]() 时,运费最少是10040元;
时,运费最少是10040元;
②当![]() 时,运费是10040元;
时,运费是10040元;
③当![]() 时,
时,![]()
∴当![]() 最大时,运费最少.即当
最大时,运费最少.即当![]() 时,运费最少.
时,运费最少.
综上: 当![]() 时,
时,![]() 城肥料全部运往
城肥料全部运往![]() 乡,B城运往
乡,B城运往![]() 城240吨,运往
城240吨,运往![]() 乡60吨,运费最少;
乡60吨,运费最少;
当![]() 时,不管
时,不管![]() 城肥料运往
城肥料运往![]() 乡多少吨,运费都是10040元.
乡多少吨,运费都是10040元.
当![]() 时,
时,![]() 城肥料全部运往
城肥料全部运往![]() 乡,
乡,![]() 城运往
城运往![]() 城40吨,运往
城40吨,运往![]() 乡260吨,运费最少.
乡260吨,运费最少.


科目:初中数学 来源: 题型:
【题目】泉州市旅游资源丰富,①清源山、②开元寺、③崇武古城三个景区是人们节假日玩的热点景区,张老师对八(1)班学生“五·一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B,游两个景区;C,游一个景区:D,不到这三个景区游玩现根据调查结果绘制了不完整的条形统计图和廟形统计图,请结合图中信息解答下列问题:
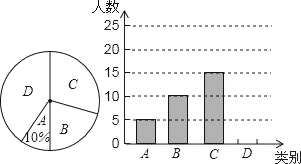
(1)八(1)班共有学生 人在扇形统计图中,表示“B类别的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)若小华、小刚两名同学,各自从三个最区中随机选一个作为5月1日游玩的景区,请用树状图或列表法求他们选中同个景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班6个合作小组的人数分别是4,6,4,5,7,8,现第4小组调出1人去第2小组,则新各组人数分别为:4,7,4,4,7,8,下列关于调配后的数据说法正确的是( )
A. 调配后平均数变小了B. 调配后众数变小了
C. 调配后中位数变大了D. 调配后方差变大了
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西宁市教育局自实施新课程改革后,学生的自主学习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下不完整的统计图,请你根据统计图解答下列问题:
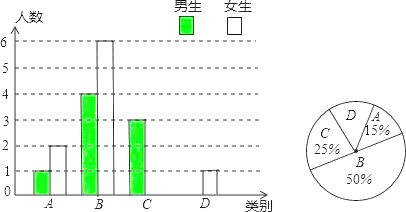
(1)本次调查中,张老师一共调查了 名同学;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法列出所有等可能的结果,并求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=﹣
的图象经过点A,反比例函数y2=﹣![]() 的图象经过点B,则m的值是( )
的图象经过点B,则m的值是( )

A.m=3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y=kx+b 的图像如图所示,则当kx+b>0 时,x 的取值范围为___________.

【答案】x>1
【解析】分析:题目要求 kx+b>0,即一次函数的图像在x 轴上方时,观察图象即可得x的取值范围.
详解:
∵kx+b>0,
∴一次函数的图像在x 轴上方时,
∴x的取值范围为:x>1.
故答案为:x>1.
点睛:本题考查了一次函数与一元一次不等式的关系,主要考查学生的观察视图能力.
【题型】填空题
【结束】
16
【题目】菱形ABCD中, ![]() ,其周长为32,则菱形面积为____________.
,其周长为32,则菱形面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
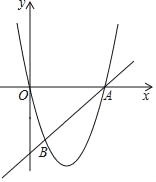
【题目】如图,在平面直角坐标系xOy中,直线AB与抛物线y=ax2+bx交于点A(6,0)和点B(1,﹣5).
(1)求这条抛物线的表达式和直线AB的表达式;
(2)如果点C在直线AB上,且∠BOC的正切值是![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com