
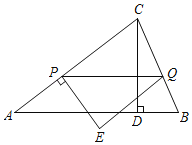
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨AB£ΩAC£Ω5£¨CD°ÕAB”⁄µ„D£¨CD£Ω3£Æµ„P¥”µ„A≥ˆ∑¢—ÿœþ∂ŒAC“‘√ø√Î1∏ˆµ•ŒªµƒÀŸ∂»œÚ÷’µ„C‘À∂Ø£Æπ˝µ„P◊˜PQ°ŒABΩªBC”⁄µ„Q£¨π˝µ„P◊˜ACµƒ¥πœþ£¨π˝µ„Q◊˜ACµƒ∆Ω––œþ£¨¡ΩœþΩª”⁄µ„E£Æ…˵„Pµƒ‘À∂Ø ±º‰Œ™t√ΣÆ
£®1£©«Ûœþ∂ŒPQµƒ≥§£Æ£®”√∫¨tµƒ¥˙ ˝ Ω±Ì æ£©
£®2£©µ±µ„E¬‰‘⁄±þAB…œ ±£¨«Ûtµƒ÷µ£Æ
£®3£©µ±°˜PQE”ΰ˜ACD÷ÿµ˛≤ø∑÷Õº–Œ «Àƒ±þ–Œ ±£¨÷±Ω”–¥≥ˆtµƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©PQ£Ω5©Åt£ª£®2£©t£Ω![]() £ª£®3£©0£ºt°Ð1ªÚ
£ª£®3£©0£ºt°Ð1ªÚ![]() °Ðt£º5
°Ðt£º5
°æΩ‚Œˆ°ø
£®1£©”…“‚µ√≥ˆPC£ΩAC©ÅAP£Ω5©Åt£¨”…PQ°ŒAB£¨µ√≥ˆ°˜PQC°◊°˜ABC£¨¿˚”√œýÀ∆»˝Ω«–Œ∂‘”¶±þ≥…±»¿˝º¥ø…«Ûµ√PQ£Ω5©Åt£ª
£®2£©µ±µ„E¬‰‘⁄±þAB…œ ±£¨‘⁄![]() ÷–£¨«Ûµ√AD£Ω4£¨cos°œCAD£Ω
÷–£¨«Ûµ√AD£Ω4£¨cos°œCAD£Ω![]() £¨‘⁄
£¨‘⁄![]() ÷–£¨cos°œCAD
÷–£¨cos°œCAD![]() £¨Õ∆≥ˆAE
£¨Õ∆≥ˆAE![]() £¨”…PQ°ŒAB£¨EQ°ŒAC£¨µ√≥ˆÀƒ±þ–ŒAEQP «∆Ω––Àƒ±þ–Œ£¨‘ÚPQ£ΩAE£¨º¥5©Åt£Ω
£¨”…PQ°ŒAB£¨EQ°ŒAC£¨µ√≥ˆÀƒ±þ–ŒAEQP «∆Ω––Àƒ±þ–Œ£¨‘ÚPQ£ΩAE£¨º¥5©Åt£Ω![]() £¨º¥ø…µ√≥ˆΩ·π˚£ª
£¨º¥ø…µ√≥ˆΩ·π˚£ª
£®3£©µ±µ„E°¢D°¢Q»˝µ„π≤œþ ±£¨”…PQ°ŒAB£¨EQ°ŒAC£¨µ√≥ˆÀƒ±þ–ŒADQP «∆Ω––Àƒ±þ–Œ£¨‘ÚPQ£ΩAD£Ω4£¨º¥5©Åt£Ω4£¨µ√≥ˆt£Ω1£¨‘Úµ±°˜PQE”ΰ˜ACD÷ÿµ˛≤ø∑÷Õº–Œ «Àƒ±þ–Œ ±£¨0£ºt°Ð1£ªµ±µ„E¬‰‘⁄±þAB…œ ±£¨”…£®2£©µ√t£Ω![]() £¨AE£ΩPQ£Ω
£¨AE£ΩPQ£Ω![]() £ºAD£¨µ√≥ˆµ„P‘⁄µΩ¥Ôµ„C«∞£¨µ„E º÷’‘⁄CDµƒ◊Û±þ£¨º¥
£ºAD£¨µ√≥ˆµ„P‘⁄µΩ¥Ôµ„C«∞£¨µ„E º÷’‘⁄CDµƒ◊Û±þ£¨º¥![]() °Ðt£º5£Æ
°Ðt£º5£Æ
£®1£©°þAB£ΩAC£Ω5£¨µ„P¥”µ„A≥ˆ∑¢—ÿœþ∂ŒAC“‘√ø√Î1∏ˆµ•ŒªµƒÀŸ∂»œÚ÷’µ„C‘À∂Ø£¨µ„Pµƒ‘À∂Ø ±º‰Œ™t√Σ¨
°ýPC£ΩAC©ÅAP£Ω5©Åt£¨
°þPQ°ŒAB£¨
°ý°˜PQC°◊°˜ABC£¨
°ý![]()
º¥£∫![]()
°ýPQ£Ω5©Åt£ª
£®2£©µ±µ„E¬‰‘⁄±þAB…œ ±£¨»ÁÕº1À˘ æ£∫

‘⁄Rt°˜ACD÷–£¨°œADC£Ω90°„£¨
AD![]() £¨
£¨
°ýcos°œCAD![]() £¨
£¨
‘⁄Rt°˜APE÷–£¨°œAPE£Ω90°„£¨cos°œCAD![]() £¨
£¨
°ý![]() £¨
£¨
°ýAE![]() AP
AP![]() £¨
£¨
°þPQ°ŒAB£¨EQ°ŒAC£¨
°ýÀƒ±þ–ŒAEQP «∆Ω––Àƒ±þ–Œ£¨
°ýPQ£ΩAE£¨
º¥£∫5©Åt£Ω![]() £¨
£¨
Ω‚µ√£∫t![]() £ª
£ª
£®3£©µ±µ„E°¢D°¢Q»˝µ„π≤œþ ±£¨»ÁÕº2À˘ æ£∫

°þPQ°ŒAB£¨EQ°ŒAC£¨
°ýÀƒ±þ–ŒADQP «∆Ω––Àƒ±þ–Œ£¨
°ýPQ£ΩAD£Ω4£¨
°ý5©Åt£Ω4£¨
°ýt£Ω1£¨
°ýµ±°˜PQE”ΰ˜ACD÷ÿµ˛≤ø∑÷Õº–Œ «Àƒ±þ–Œ ±£¨0£ºt°Ð1£ª
µ±µ„E¬‰‘⁄±þAB…œ ±£¨»ÁÕº1À˘ 棨
”…£®2£©µ√£∫t![]() £¨
£¨
AE£ΩPQ£Ω5©Å![]() £ºAD£¨
£ºAD£¨
°ýµ„P‘⁄µΩ¥Ôµ„C«∞£¨µ„E º÷’‘⁄CDµƒ◊Û±þ£¨
°þAC£Ω5£¨
°ýt£º5£¨
°ý![]() °Ðt£º5£¨
°Ðt£º5£¨
◊€…œ£∫µ±°˜PQE”ΰ˜ACD÷ÿµ˛≤ø∑÷Õº–Œ «Àƒ±þ–Œ ±£¨tµƒ»°÷µ∑∂ŒßŒ™0£ºt°Ð1ªÚ![]() °Ðt£º5£Æ
°Ðt£º5£Æ


 –°ÃÏ≤≈øŒ ±◊˜“µœµ¡–¥∞∏
–°ÃÏ≤≈øŒ ±◊˜“µœµ¡–¥∞∏ “ªøŒÀƒ¡∑œµ¡–¥∞∏
“ªøŒÀƒ¡∑œµ¡–¥∞∏ ª∆∏‘–°◊¥‘™¬˙∑÷≥¥Ì¢≤‚—Èœµ¡–¥∞∏
ª∆∏‘–°◊¥‘™¬˙∑÷≥¥Ì¢≤‚—Èœµ¡–¥∞∏ –¬∏®Ωõº—ßœµ¡–¥∞∏
–¬∏®Ωõº—ßœµ¡–¥∞∏ —Ùπ‚Õ¨—ß“ªœþ√˚ ¶»´”≈∫√æÌœµ¡–¥∞∏
—Ùπ‚Õ¨—ß“ªœþ√˚ ¶»´”≈∫√æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþAC£∫y£Ω©Å3x+3![]() ”Î÷±œþAB£∫y£Ωax+bΩª”⁄µ„A£¨«“B£®©Å9£¨0£©£Æ
”Î÷±œþAB£∫y£Ωax+bΩª”⁄µ„A£¨«“B£®©Å9£¨0£©£Æ
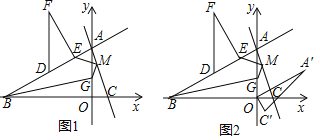
£®1£©»ÙF «µ⁄∂˛œÛœÞŒª”⁄÷±œþAB…œ∑Ωµƒ“ªµ„£¨π˝F◊˜FE°ÕAB”⁄E£¨π˝F◊˜FD°Œy÷·Ωª÷±œþAB”⁄D£¨DŒ™AB÷–µ„£¨∆‰÷–°˜DFFµƒ÷Ð≥§ «12+4![]() £¨»ÙMŒ™œþ∂ŒAC…œ“ª∂ص„£¨¡¨Ω”EM£¨«ÛEM+
£¨»ÙMŒ™œþ∂ŒAC…œ“ª∂ص„£¨¡¨Ω”EM£¨«ÛEM+![]() MCµƒ◊Ó–°÷µ£¨¥À ±y÷·…œ”–“ª∏ˆ∂ص„G£¨µ±|BG©ÅMG|◊Ó¥Û ±£¨«ÛGµ„◊¯±Í£ª
MCµƒ◊Ó–°÷µ£¨¥À ±y÷·…œ”–“ª∏ˆ∂ص„G£¨µ±|BG©ÅMG|◊Ó¥Û ±£¨«ÛGµ„◊¯±Í£ª
£®2£©‘⁄£®1£©µƒ«Èøˆœ¬£¨Ω´°˜AOC»∆Oµ„À≥ ±’Ζ˝◊™60°„∫Ûµ√µΩ°˜A°‰OC'£¨»ÁÕº2£¨Ω´œþ∂ŒOA°‰—ÿ◊≈x÷·∆Ω“∆£¨º«∆Ω“∆π˝≥Ã÷–µƒœþ∂ŒOA°‰Œ™O°‰A°Â£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷– «∑ҥʑ⁄µ„P£¨ πµ√“‘µ„O°‰£¨A°Â£¨E£¨PŒ™∂•µ„µƒÀƒ±þ–ŒŒ™¡‚–Œ£¨»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„Pµƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–°¡¡°¢–°∑º∫Õ¡Ω∏ˆƒ∞…˙»Àº◊°¢““Õ¨‘⁄»ÁÕºÀ˘ 浃µÿœ¬≥µø‚µ»µÁÃ𣨓—÷™¡Ω∏ˆƒ∞…˙»ÀµΩ1÷¡4 ≤„µƒ»Œ“‚“ª≤„≥ˆµÁÃð£¨≤¢…˺◊‘⁄a≤„≥ˆµÁÃ𣨓“‘⁄b≤„≥ˆµÁÃð£Æ
£®1£©«Îƒ„”√ª≠ ˜◊¥ÕºªÚ¡–±Ì∑®«Û≥ˆº◊°¢““∂˛»À‘⁄Õ¨“ª≤„¬•≥ˆµÁÃðµƒ∏≈¬ £ª
£®2£©–°¡¡∫Õ–°∑º¥Ú∂ƒÀµ£∫°∞»Ùº◊°¢““‘⁄Õ¨“ª≤„ªÚœý¡⁄¬•≤„≥ˆµÁÃ𣨑ږ°¡¡ §£¨∑Ò‘Ú–°∑º §°±£Æ∏√”Œœ∑ «∑Òπ´∆Ω£øÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y£Ωax2£´bx£´c£®a£º0£ºb£©µƒÕºœÒ”Îx÷·÷ª”–“ª∏ˆΩªµ„£¨œ¬¡–Ω·¬€£∫¢Ÿx£º0 ±£¨yÀÊx‘ˆ¥Û∂¯‘ˆ¥Û£ª¢⁄a£´b£´c£º0£ª¢€πÿ”⁄xµƒ∑Ω≥Ãax2£´bx£´c£´2£Ω0”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝∏˘£Æ∆‰÷–À˘”–’˝»∑Ω·¬€µƒ–Ú∫≈ «£® £©
A.¢Ÿ¢⁄B.¢⁄¢€C.¢Ÿ¢€D.¢Ÿ¢⁄¢€
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™¡‚–ŒABCD£¨∂‘Ω«œþAC°¢BDœýΩª”⁄µ„O£¨AC£Ω6£¨BD£Ω8£Æµ„E «AB±þ…œ“ªµ„£¨«Û◊˜æÿ–ŒEFGH£¨ πµ√µ„F°¢G°¢H∑÷±¬‰‘⁄±þBC°¢CD°¢AD…œ£Æ…Ë AE£Ωm£Æ

£®1£©»ÁÕº¢Ÿ£¨µ±m£Ω1 ±£¨¿˚”√÷±≥þ∫Õ‘≤πÊ£¨◊˜≥ˆÀ˘”–¬˙◊„Ãıº˛µƒæÿ–ŒEFGH£ª£®±£¡Ù◊˜Õº∫€º££¨≤ª–¥◊˜∑®£©
£®2£©–¥≥ˆæÿ–ŒEFGHµƒ∏ˆ ˝º∞∂‘”¶µƒmµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Àƒ±þ–Œ![]() ƒ⁄Ω””⁄
ƒ⁄Ω””⁄![]() £¨
£¨![]() «
«![]() µƒ÷±æ∂£¨
µƒ÷±æ∂£¨![]() ∆Ω∑÷
∆Ω∑÷![]() £¨π˝
£¨π˝![]() µ„◊˜
µ„◊˜![]() ”⁄
”⁄![]() µ„.
µ„.
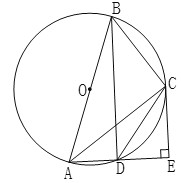
£®1£©«Û÷§£∫![]() «
«![]() µƒ«–œþ£ª
µƒ«–œþ£ª
£®2£©»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ≥§.
µƒ≥§.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABC÷–£¨AB£ΩAC£Æ
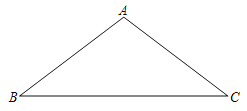
£®1£©”√ŒÞøÃ∂»µƒ÷±≥þ∫Õ‘≤πÊ◊˜°˜ABCµƒÕ‚Ω”‘≤£ª£®±£¡Ùª≠Õº∫€º££©
£®2£©»ÙAB£Ω10£¨BC£Ω16£¨«Û°˜ABCµƒÕ‚Ω”‘≤∞Îæ∂£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
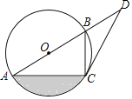
°æƒø°ø»ÁÕº£¨“—÷™AB «°—Oµƒ÷±æ∂£¨C «°—O…œµƒµ„£¨µ„D‘⁄ABµƒ—”≥§œþ…œ£¨°œBCD=°œBAC.
£®1£©«Û÷§£∫CD «°—Oµƒ«–œþ£Æ
£®2£©»Ù°œD=30°„£¨BD=2£¨«Û°—Oµƒ∞Îæ∂
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨«ÛÕº÷–“ı”∞≤ø∑÷µƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂∑√≈ƒ≥—¯÷≥ªß√øƒÍµƒ—¯÷≥≥…±æ∞¸¿®πÃ∂®≥…±æ∫Õø…±‰∂Ø≥…±æ£¨∆‰÷–πÃ∂®≥…±æ√øƒÍæ˘Œ™4ÕÚ‘™£¨ø…±‰∂Ø≥…±æ÷ƒÍ‘ˆ≥§. “—÷™∏√—¯÷≥ªßµ⁄1ƒÍµƒø…±‰∂Ø≥…±æŒ™2ÕÚ‘™£¨…Ëø…±‰∂Ø≥…±æµƒƒÍ∆Ωæ˘‘ˆ≥§¬ Œ™x.
(1)”√∫¨xµƒ¥˙ ˝ Ω±Ì æµ⁄2ƒÍµƒø…±‰∂Ø≥…±æ£∫ ÕÚ‘™£ª
(2)»Áπ˚∏√—¯÷≥ªßµ⁄3ƒÍµƒ≥…±æŒ™6.42ÕÚ‘™£¨«Ûø…±‰∂Ø≥…±æµƒƒÍ∆Ωæ˘‘ˆ≥§¬ .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com