【题目】某商场将每件进价为
元的某种商品原来按每件
元出售，一天可售出件．后来经过市场调查，发现这种商品单价每降低
元，其销量可增加
件．
求商场经营该商品原来一天可获利润多少元？
若商场经营该商品一天要获利润
元，并让顾客得到实惠，则每件商品应降价多少元？
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝
，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝_____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，E是ABCD的边CD的中点，延长AE交BC的延长线于点F．
（1）求证：△ADE≌△FCE．
（2）若∠BAF=90°，BC=5，EF=3，求CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
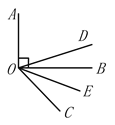
【题目】如图，DO平分∠AOC，OE平分∠BOC，若OA⊥OB，
（1）当∠BOC＝30°，∠DOE＝_______________； 当∠BOC＝60°，∠DOE＝_______________；
（2）通过上面的计算，猜想∠DOE的度数与∠AOB有什么关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的“探究”
（提出问题）三个有理数a、b、c满足abc＞0，求
的值．
（解决问题）
解：由题意得：a，b，c三个有理数都为正数或其中一个为正数，另两个为负数．
①a，b，c都是正数，即a＞0，b＞0，c＞0时，
则：=
=1+1+3；
②当a，b，c有一个为正数，另两个为负数时，设a＞0，b＜0，c＜0，
则：=
=1+（﹣1）+（﹣1）=﹣1
所以的值为3或﹣1．
（探究）请根据上面的解题思路解答下面的问题：
（1）三个有理数a，b，c满足abc＜0，求的值；
（2）已知|a|=3，|b|=1，且a＜b，求a+b的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）先完成下列表格：
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | ______ | 1 | ______ | ______ | …… |
（2）由上表你发现什么规律？
（3）根据你发现的规律填空：
①已知
=1.732则
=______
=______
②已知
=0.056，则
=______
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】盒中有x个黑球和y个白球，这些球除颜色外无其他差别．从盒中随机取一个球，它是黑球的概率是
；往盒中再放进1个黑球，这时取得黑球的概率变为
.
(1)试求出x和y的值；
(2)小王和小林利用x个黑球和y个白球进行摸球游戏．约定：从盒中随机摸取一个，接着从剩下的球中再随机摸取一个，若两球颜色相同则小王胜，若颜色不同则小林胜．游戏公平吗？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,已知∠BDG+∠EFG=180°,∠DEF=∠B,试判断∠AED与∠C的大小关系,并加以说明.
解:∠AED=∠C.
理由:∵∠EFD+∠EFG=180°( ),
∠BDG+∠EFG=180°(已知)
∴∠BDG =∠EFD ( ),
∴BD∥EF( ),
∴∠BDE+∠DEF =180°( ).
又∵∠DEF=∠B( ),
∴∠BDE+∠B =180°( ),
∴DE∥BC( ),
∴∠AED=∠C( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
