
郑州市花卉种 植专业户王有才承包了30亩花圃,分别种植
植专业户王有才承包了30亩花圃,分别种植 康乃馨
康乃馨 和玫瑰花,有关成本、销售额见下表:
和玫瑰花,有关成本、销售额见下表:
| 种植种类 | 成本(万元/亩) | 销售额(万元/亩) |
| 康乃馨 | 2.4 | 3 |
| 玫瑰花 | 2 | 2.5 |
(1)2012年,王有才种植康乃馨20亩、 玫瑰花10亩,求王有才这一年共
玫瑰花10亩,求王有才这一年共 收益多少万元?(收益=销售额-成本)
收益多少万元?(收益=销售额-成本)
(2)2013年,王有才继续用这30亩花圃全部种植康乃馨和玫瑰花,计划投入成本不超过70万元.若每亩种植的成本 、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花
、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花 各多少亩?
各多少亩?
(3)已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg,根据(2)中的种植亩数,为了节约运输成本,实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍,结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克?
(1)17万元;(2)康乃馨25亩,玫瑰花5亩;(3)4000千克
【解析】

答:要获得最大收益,应养殖康乃馨25亩, 玫瑰花5亩;
玫瑰花5亩;
(3)设王有才原定的 运输车辆每次可装载饲料a㎏
运输车辆每次可装载饲料a㎏
由(2)得,共需要饲料为500×25+700×5=16000(㎏),
根据题意得
 ,解得
,解得 a=4000,
a=4000,
把a=4000代入原方程公分母得,2a=2×4000=8000≠0,
故a=4000是原方程的解.
答:王有才原定的运输车辆每次可装载饲料4000㎏.
考点:一次函数的应用,分式方程的应用,一元一次不等式的应用
点评:解题的关键是列不等式求x的取值范围,再表示出函数关系求最大值,再列分式方 程求解.
程求解.


科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)(0,2)(4,2),直线l的解析式为y = kx+5-4k(k > 0).

(1)当直线l经过点B时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点D;
(3)直线l与y轴交于点M,点N是线段DM上的一点, 且△NBD为等腰三角形,试探究:
①当函数y = kx+5-4k为正比例函数时,点N的个数有 个;
② 点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
在新农村建设中,某乡镇决定对一段长600 0米的公路进行修建改造。根据需要,该工程在实际施工时增加了施工人员,每天修建的公路比原计划增加了50%,结果
0米的公路进行修建改造。根据需要,该工程在实际施工时增加了施工人员,每天修建的公路比原计划增加了50%,结果 提前4天完成任务。设现在每天修建x米,那么下面所列方程中正确的是【 】
提前4天完成任务。设现在每天修建x米,那么下面所列方程中正确的是【 】 。
。
A. 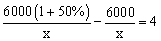 B.
B. 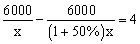
C.  D.
D. 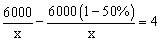
查看答案和解析>>
科目:初中数学 来源: 题型:
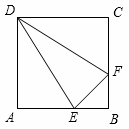
如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.若△DEF的面积为y,BF的长为x,则表示y与x的函数关系的图象大致是( )


A.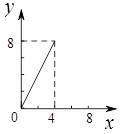

 B.
B.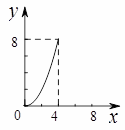

 C.
C.

 D.
D.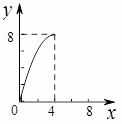


查看答案和解析>>
科目:初中数学 来源: 题型:
某校为实施 国家“营养早餐”工程,食堂用甲、乙两种
国家“营养早餐”工程,食堂用甲、乙两种 原料配制成某种
原料配制成某种 营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
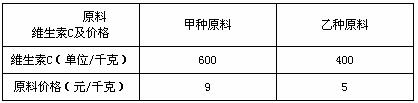
现要配制这种营养食品20千克,要求每千 克至少含有480单位的维生素C.设
克至少含有480单位的维生素C.设 购买甲种原料x千克.
购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
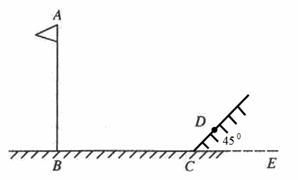
某校初三年级“数学兴趣小组”实地测量操场旗杆的高度.旗杆的影子落在操场和操场边的土坡上,如图所示,测得在操场上的影长BC=20 m,斜坡上的影长CD=2m,已知斜坡CD与操场平面的夹角为45°,同时测得身高l. 65m的学生在操场 上的影长为3.3 m.求旗杆AB的高度。(结果精确到1m)
65m的学生在操场 上的影长为3.3 m.求旗杆AB的高度。(结果精确到1m)
(提示:同一时刻物高与影长成正比.参考数据: ≈1.414.
≈1.414. ≈1.732.
≈1.732.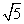 ≈2.236)
≈2.236)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com