
二次函数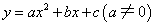
 的图象如图所示.
的图象如图所示.
有下列结论:①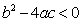
 ;②
;②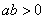
 ;③
;③
 ;④
;④
 ;⑤当
;⑤当
 时,
时,
 只能等于
只能等于
 .其中
.其中 正确的是( )
正确的是( )



B
【解析】
试题分析:由抛物线与x轴有 两个交点得到b2-4ac>0,判定①错误;
两个交点得到b2-4ac>0,判定①错误;

∴b2-4ac>0;
故本 选项错误;
选项错误;
②由图示知对称轴方程x=
 =2>0,即
=2>0,即
 <0,a、b异号,故ab<0;
<0,a、b异号,故ab<0;
故本选项错误;
③根据图示知,当x=-1时,y=0,即a-b+ c=0;
c=0;
故本选项正确;
④由图示知对称轴方程x=
 =2,即b=-4a,所以4a+b=0;
=2,即b=-4a,所以4a+b=0;
故本选项正确;
⑤∵(0,2)的对称点为(4,2),
∴当y=2时,x =0或2;
=0或2;
故本选项错误;
综上所述,正确的说法有③④;
故选B.
考点:本题主要考查图象与二次函数系数之间的关系
点评 :解答本题的关键是会利用对称轴的范围求2a与b的关系,同时熟练掌握二次函数
:解答本题的关键是会利用对称轴的范围求2a与b的关系,同时熟练掌握二次函数 与方程之间的转换,根的判别式的运用
与方程之间的转换,根的判别式的运用
A.①④ B.③ ④ C.②⑤ D.③⑤
④ C.②⑤ D.③⑤


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
郑州市花卉种 植专业户王有才承包了30亩花圃,分别种植
植专业户王有才承包了30亩花圃,分别种植 康乃馨
康乃馨 和玫瑰花,有关成本、销售额见下表:
和玫瑰花,有关成本、销售额见下表:
| 种植种类 | 成本(万元/亩) | 销售额(万元/亩) |
| 康乃馨 | 2.4 | 3 |
| 玫瑰花 | 2 | 2.5 |
(1)2012年,王有才种植康乃馨20亩、 玫瑰花10亩,求王有才这一年共
玫瑰花10亩,求王有才这一年共 收益多少万元?(收益=销售额-成本)
收益多少万元?(收益=销售额-成本)
(2)2013年,王有才继续用这30亩花圃全部种植康乃馨和玫瑰花,计划投入成本不超过70万元.若每亩种植的成本 、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花
、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花 各多少亩?
各多少亩?
(3)已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg,根据(2)中的种植亩数,为了节约运输成本,实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍,结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
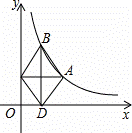
 如图所示,点A是双曲线y=
如图所示,点A是双曲线y=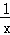 (x>0)上的一动点,过A作AC⊥y轴
(x>0)上的一动点,过A作AC⊥y轴 ,垂足为点C,作AC的垂直平分线双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,四边形ABCD的面积( )
,垂足为点C,作AC的垂直平分线双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,四边形ABCD的面积( )
A.逐渐变小 B.由大变小再由小变大
C.由 小变大再有大变小 D.不变
小变大再有大变小 D.不变
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m) 与运行的水平距离x(m)满足关系式
与运行的水平距离x(m)满足关系式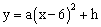 。已知球网与O点
。已知球网与O点 的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围);
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求 二次函数中二次项系数a的最大值。
二次函数中二次项系数a的最大值。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线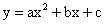
 过点B。
过点B。
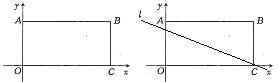
(1)若a=-l,且抛物线与矩形有且只有三个交点B、D、E,求△ BDE的面积S的最大值;
(2)若抛物线与矩形有且只有三个交点B 、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
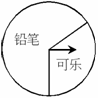
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指 针落在哪
针落在哪 一区域就可以获得相应的奖品.下表是活动进
一区域就可以获得相应的奖品.下表是活动进 行中的一组统计数据:
行中的一组统计数据:

(1)计算并完成表格:


(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获得铅笔的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①是3×3菱形格,将其中 两个格子涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕菱形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有【 】
两个格子涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕菱形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有【 】
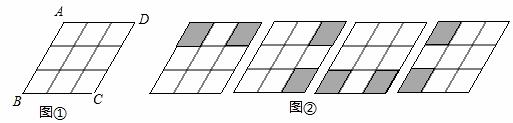
A.4种  B.5种 C.6种 D.7种
B.5种 C.6种 D.7种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com