D。
字词句段篇系列答案科目：初中数学 来源： 题型：
如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（ ）
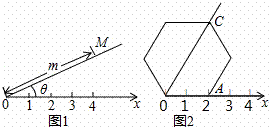
A．（60°，4） B．（45°，4） C．（60°，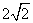
） D．（50°，）
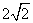查看答案和解析>>
科目：初中数学 来源： 题型：
某校为实施
国家“营养早餐”工程，食堂用甲、乙两种
原料配制成某种营养食品，已知这两种原料的维生素C含量及购买这两种原料的价格如下表：
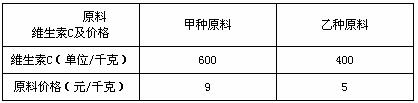
现要配制这种营养食品20千克，要求每千克至少含有480单位的维生素C．设购买甲种原料x千克．
（1）至少需要购买甲种原料多少千克？
（2）设食堂用于购买这两种原料的总费用为y元，求y与x的函数关系式．并说明购买甲种原料多少千克时，总费用最少？
查看答案和解析>>
科目：初中数学 来源： 题型：
某山区的一种特产由于运输原因，长期只能在当地销售，当地政府对该特产的销售投资收益为：每投入x万元，可获得利润P=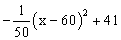
（万元）。当地政府拟规划加快开
发该特产的销售，其规划方案为：在规划前后对该项目每年最多可投人100万元的销售投资，在实施规划5年的前两
年中，每年都从100万元中拨出60万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的3年中，该特产既在本地销售，也在外地销售。
在外地销售的投资收益为：每投入
万元，可获利润Q=
（万元）。
（1）若不进行开发，求5年所获利润的最大值是多少？
（2）若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？
（3）根据（1）、（2），该方案是否具有实施价值？
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：y关于x的函数
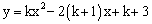的图象与x轴有交点。
（1）求k的取值范围；
（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足
．
①求k的值；②当
时，请结合函数图象确定y的最大值和最小值。
查看答案和解析>>
科目：初中数学 来源： 题型：
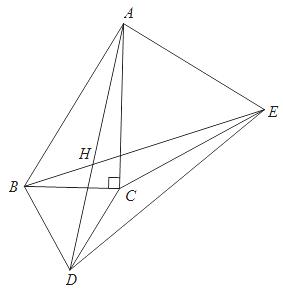
如图，分别以
Rt△ABC的斜两条直角边为边向△ABC外作等边△BCD和等边△ACE， AD与BE交于点H，∠ACB=90°。
（1）求证：AD=BE；
（2）求∠AHE的度数；
（3）若∠BAC=30°，BC=1，求DE的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图象交反比例函数
的图象于点A、B，交
轴于点C。
的取值范围；
＝
，求
恰好只有5个正整数解，则m的取值范围是 。
，则函数
和
的图象大致是【 】
B. 
C. 
D. 
的图象如图所示．
；②
；③
；④
；⑤当
时，
只能等于
．其中
正确的是（ ）
