
已知:y关于x的函数
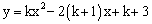 的图象与x轴有交点。
的图象与x轴有交点。
(1)求k的取值范围;
(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足 .
.
①求k的值;②当 时,请结合函数图象确定y的最大值和最小值。
时,请结合函数图象确定y的最大值和最小值。
(1)当k=0时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点。
当k≠0时, 函数为二次函数,其图象与x轴
函数为二次函数,其图象与x轴 有一个或两个交点,
有一个或两个交点,
令y=0得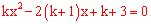 .
.
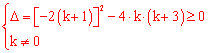 ,解得
,解得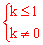 。
。
综上所述,k的取值范围是k≤1。
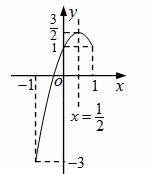 (2)①∵x1≠x2,由(1)知k<1且k≠0。
(2)①∵x1≠x2,由(1)知k<1且k≠0。
由题意得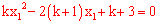 ,即
,即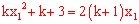 (*),
(*),
将(*)代入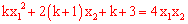 中得:
中得: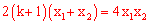 。
。
又∵x1+x2=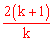 ,x1x2=
,x1x2=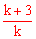 ,∴
,∴ ,
,
解得:k1=﹣2,k2=1(不合题意,舍去)。∴所求k值为﹣2。
②如图,∵k=﹣2,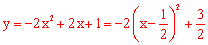 ,且﹣1≤x≤1,
,且﹣1≤x≤1,
由图象知:当x=﹣1时,y最小=﹣ 3;当x=
3;当x=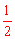 时,y最大=
时,y最大=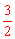 。
。
∴y的最大值为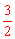 ,最小值为﹣3。
,最小值为﹣3。
【考点】抛物线与x轴的交点,一次函数的定义,一元二次方程根的判别式和根与系数物关系,二次函数的最值,分类思想和数形结合思想的应用。



科目:初中数学 来源: 题型:
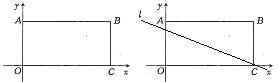
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线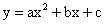
 过点B。
过点B。
(1)若a=-l,且抛物线与矩形有且只有三个交点B、D、E,求△ BDE的面积S的最大值;
(2)若抛物线与矩形有且只有三个交点B 、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指 针落在哪
针落在哪 一区域就可以获得相应的奖品.下表是活动进
一区域就可以获得相应的奖品.下表是活动进 行中的一组统计数据:
行中的一组统计数据:

(1)计算并完成表格:


(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获得铅笔的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
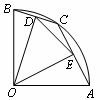
如图,在半径为2的扇形OAB中,∠AOB=90°,点C是弧AB上的—个动点(不与A, B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )
B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )

A.1 B.2 C.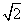
 D.
D.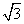

查看答案和解析>>
科目:初中数学 来源: 题型:
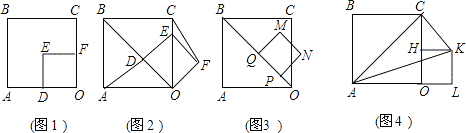
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向 旋转45
旋转45 °得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正 方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正
方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正 方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com