如图，矩形ABCD的BC边在直线l上，AD=5，AB=3， P为直线l上的点，且△AEP是腰长为5的等腰三角形，则
BP= 
科目：初中数学 来源： 题型：
某山区的一种特产由于运输原因，长期只能在当地销售，当地政府对该特产的销售投资收益为：每投入x万元，可获得利润P=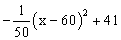
（万元）。当地政府拟规划加快开
发该特产的销售，其规划方案为：在规划前后对该项目每年最多可投人100万元的销售投资，在实施规划5年的前两
年中，每年都从100万元中拨出60万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的3年中，该特产既在本地销售，也在外地销售。
在外地销售的投资收益为：每投入
万元，可获利润Q=
（万元）。
（1）若不进行开发，求5年所获利润的最大值是多少？
（2）若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？
（3）根据（1）、（2），该方案是否具有实施价值？
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：y关于x的函数
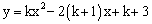的图象与x轴有交点。
（1）求k的取值范围；
（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足
．
①求k的值；②当
时，请结合函数图象确定y的最大值和最小值。
查看答案和解析>>
科目：初中数学 来源： 题型：
有三张正面分别
写有数
字﹣2，﹣1，1的卡片，它们的背面完全相
同，将这
三张卡片北背面朝上洗匀后随机抽取一张，以其正面的数字作为x的值，不放回卡片洗匀，再从余下的两张卡片中随机抽取
一张，以其正面的数字作为y的值，两次结果记为（x，y）。
（1）用树状
图或列表法表示（x，y）所有可能出现的结果；
（2）求使分式
无意义的（x，y）出现的概率；
（3）化简分式，并求使分式的值为整数的（x，y）出现的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
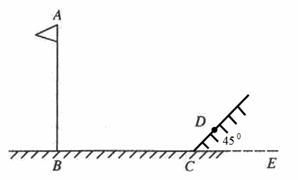
某校初三年级“数学兴趣小组”实地测量操场旗杆的高度．旗杆的影子落在操场和操场边的土坡上，如图所示，测得在操场上的影长BC=20 m，斜坡上的影长CD=2m，已知斜坡CD与操场平面的夹角为45°，同时测得身高l.65m的学生在操场 上的影长为3.3 m．求旗杆AB的高度。(结果精确到1m)
(提示：同一时刻物高与影长成正比．参考数据：
≈1.414．
≈1.732．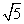
≈2.236)
查看答案和解析>>
科目：初中数学 来源： 题型：
矩形、菱形、正方形都是平行四边形，但它们都是有特殊条件的平行四边形，正方形不仅是特殊的矩形，也是特殊的菱形.因此，我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题：
（
1）将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
（2）要证明一个四边形是正方形，可先证明四边形是矩形，再证明这个矩形的_______相等；或者先证明四边形是菱形，在证明这个菱形有一个角是________ .
（3）某同学根据菱形面积计算公式推导出对角线长
为a的正方形面积是S=0.5a2，对此结论，你认为是否正确？若正确，请说
明理由；若不正确，请举出一个反例说明.
查看答案和解析>>
科目：初中数学 来源： 题型：
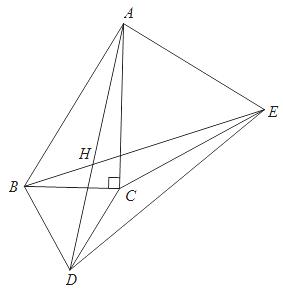
如图，分别以
Rt△ABC的斜两条直角边为边向△ABC外作等边△BCD和等边△ACE， AD与BE交于点H，∠ACB=90°。
（1）求证：AD=BE；
（2）求∠AHE的度数；
（3）若∠BAC=30°，BC=1，求DE的长
查看答案和解析>>
科目：初中数学 来源： 题型：
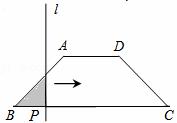
如下图所示，已知等腰梯形ABCD，AD∥BC，AD=2，BC=
6，AB=DC=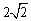
，若动直线l垂直于BC，且从经过点B的位置向右平移，直至经过点C的位置停止，设扫过的阴影部分的面积为S
，BP为x，则S关于x的函数关系式是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
恰好只有5个正整数解，则m的取值范围是 。