
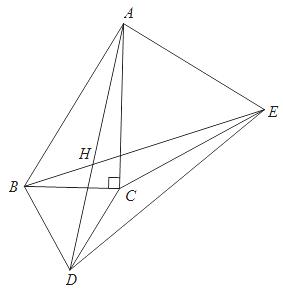
如图,分别以 Rt△ABC的斜两条直角边为边向△ABC外作等边△BCD和等边△ACE, AD与BE交于点H,∠ACB=90°。
Rt△ABC的斜两条直角边为边向△ABC外作等边△BCD和等边△ACE, AD与BE交于点H,∠ACB=90°。
(1)求证:AD=BE;
(2)求∠AHE的度数;
(3)若∠BAC=30°,BC=1,求DE的长
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
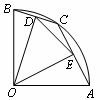
如图,在半径为2的扇形OAB中,∠AOB=90°,点C是弧AB上的—个动点(不与A, B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )
B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )

A.1 B.2 C.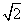
 D.
D.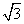

查看答案和解析>>
科目:初中数学 来源: 题型:
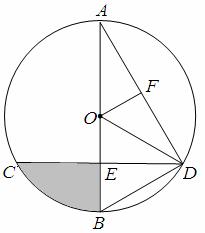
如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AD于F,△OBD是等边三角形。
(1)求证:OF∥ BD;
BD;
(2)求证:△AFO≌△D EB;
EB;
(3)若BE=4cm, 求阴影部分的面积。
求阴影部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
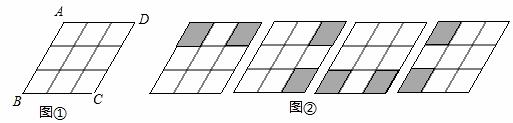
如图①是3×3菱形格,将其中 两个格子涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕菱形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有【 】
两个格子涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕菱形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有【 】
A.4种  B.5种 C.6种 D.7种
B.5种 C.6种 D.7种
查看答案和解析>>
科目:初中数学 来源: 题型:
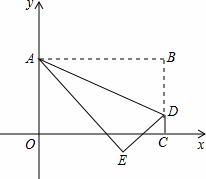
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形 OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m=
OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m= ,点E的坐标为 ;
,点E的坐标为 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
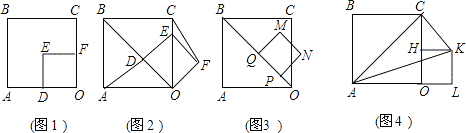
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向 旋转45
旋转45 °得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正 方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正
方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正 方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
两个全等的梯形纸片如图(1)摆放,将梯形纸片ABCD沿上底AD方向向右平移得到图(2).已知AD=4,BC=8,若 阴影部分的面积等于四边形A′B′BA的面积,则图(2)中平移距离A′A= .
阴影部分的面积等于四边形A′B′BA的面积,则图(2)中平移距离A′A= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com