
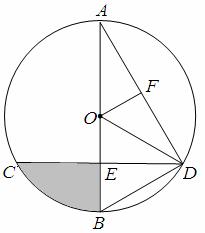
如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AD于F,△OBD是等边三角形。
(1)求证:OF∥ BD;
BD;
(2)求证:△AFO≌△D EB;
EB;
(3)若BE=4cm, 求阴影部分的面积。
求阴影部分的面积。
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
有三张正面分别 写有数
写有数 字﹣2,﹣1,1的卡片,它们的背面完全相
字﹣2,﹣1,1的卡片,它们的背面完全相 同,将这
同,将这 三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,不放回卡片洗匀,再从余下的两张卡片中随机抽取
三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,不放回卡片洗匀,再从余下的两张卡片中随机抽取 一张,以其正面的数字作为y的值,两次结果记为(x,y)。
一张,以其正面的数字作为y的值,两次结果记为(x,y)。
(1)用树状 图或列表法表示(x,y)所有可能出现的结果;
图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式 无意义的(x,y)
无意义的(x,y) 出现
出现 的概率;
的概率;
(3)化简分式 ,并求使分式的值为整数的(x,y)出现的概率.
,并求使分式的值为整数的(x,y)出现的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的矩形,也是特殊的菱形.因此,我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题:
( 1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.

(2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的_______相等;或者先证明四边形是菱形,在证明这个菱形有一个角是________ .
(3)某同学根据菱形面积计算公式推导出对角线长 为a的正方形面积是S=0.5a2,对此结论,你认为是否正确?若正确,请说
为a的正方形面积是S=0.5a2,对此结论,你认为是否正确?若正确,请说 明理由;若不正确,请举出一个反例说明.
明理由;若不正确,请举出一个反例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
在Rt△ABC中,∠A=90°,∠B=30°, AC=1,点O在BC上,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则⊙O的半径为 ;∠MND的度数为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
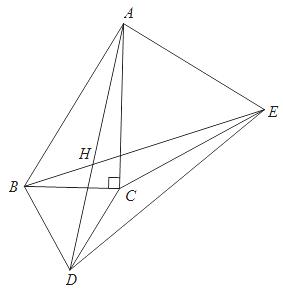
如图,分别以 Rt△ABC的斜两条直角边为边向△ABC外作等边△BCD和等边△ACE, AD与BE交于点H,∠ACB=90°。
Rt△ABC的斜两条直角边为边向△ABC外作等边△BCD和等边△ACE, AD与BE交于点H,∠ACB=90°。
(1)求证:AD=BE;
(2)求∠AHE的度数;
(3)若∠BAC=30°,BC=1,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
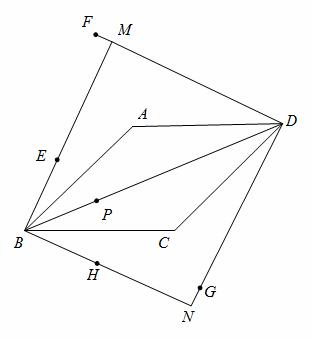
菱形ABCD中,∠ABC=450,点P是对角线BD上的任一点,点P关于直线AB、AD、CD、BC的对称点分别是点E、F、G、H, BE与DF相交于点M,DG与BH相交于点N,证明:四边形BMDN是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,对称轴为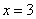
 的抛物线
的抛物线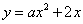
 与
与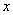
 轴相交于点
轴相交于点
 、
、



(1).求抛物线的解析式,并求出顶点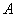
 的坐标
的坐标
(2).连结AB,把AB所在的直线平移,使它经过原点O,得到直线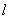
 .点P是
.点P是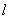
 上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为
上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为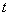
 ,当0<S≤18时,求
,当0<S≤18时,求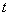
 的取值范围
的取值范围
(3).在(2)的条件下,当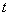
 取最大值时,抛物线上是否存在点
取最大值时,抛物线上是否存在点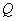
 ,使△OP
,使△OP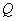
 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点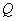
 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com