
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线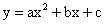
 过点B。
过点B。
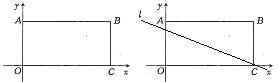
(1)若a=-l,且抛物线与矩形有且只有三个交点B、D、E,求△ BDE的面积S的最大值;
(2)若抛物线与矩形有且只有三个交点B 、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
(1)∵a=-l,∴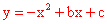 。
。
又 ∵抛物线
∵抛物线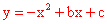 过点B(6,3),∴
过点B(6,3),∴ ,即
,即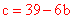 。
。
∴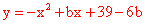
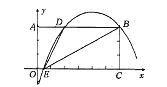
如图① ,当抛物线与矩形的两个交点D、E分别在AB、OC边上时, 抛物线与y轴的交点应落在原点或原点下方。
∴ 当x=0时,y≤0。
∴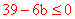 ,即
,即
 。
。
由抛物线的对称性可知:  。
。
又∵ △ BDE的高=BC=3,∴ S= 。
。
∵  >0,∴ S随b的增大而减少。
>0,∴ S随b的增大而减少。
∴ 当b=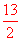 时,S的最大值=
时,S的最大值=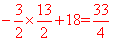 。
。
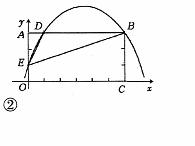
如图② ,当抛物线与矩 形的两个交点D、E分别在AB、AO边上时,抛物线与直线x=0的交点应落在线段AO上且
形的两个交点D、E分别在AB、AO边上时,抛物线与直线x=0的交点应落在线段AO上且 不与点A重合,即0≤
不与点A重合,即0≤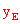 <3。
<3。
当x=0,则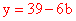 ,∴ 0≤
,∴ 0≤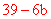 <3,∴
<3,∴ 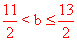 。
。
∴ AE =
= 。
。
∴ S=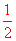 BD·AE=
BD·AE= 。
。
∵ 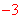 <0,∴ S随b的增大而增大。
<0,∴ S随b的增大而增大。
∴ 当b=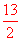 时,S的最大值=
时,S的最大值= 。
。
综上所述:S的最大值为 。
。
(2)当a>0时,符合题意要求的抛物线不存在。

 当a<0时,符合题意要求的抛物线有两种情况:
当a<0时,符合题意要求的抛物线有两种情况:
① 当点M、N分别在AB、OC边上时.
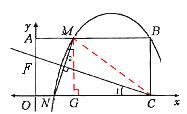
如图③ ,过M点作MG⊥ OC于点G,连接CM,
∴ MG=OA=3.∠2+∠ MNG=90°。
∵ CF垂直平分MN.
∴ CM=CN,∠1+∠ MNG=90°,∠ 1=∠ 2。
∵ AF=1,OF=3-1=2。
∴  ,
, 。
。
∴ GN=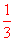 GM=1。
GM=1。
设N(n,0),则G(n+1,0),∴ M(n+1,3 )。 ∴ BM=
)。 ∴ BM=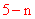 ,CM=CN=
,CM=CN=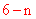 。
。
在Rt△BCM中,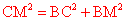 ,
,
∴ 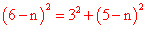 ,解得n=1。∴ M(2,3),N(1,0)。
,解得n=1。∴ M(2,3),N(1,0)。
把M(2,3),N(1,0),B(6,3)分别代入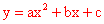
 ,得
,得
 ,解得
,解得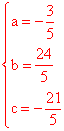 。
。
∴抛物线的解析式 为
为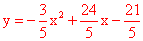 。
。
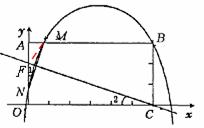

设N(0,n).则FN=2-n,AN=3一n。∴MF=2-n,AM= 。
。
在Rt △MABF中,∵
△MABF中,∵
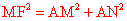 ,∴
,∴ 。
。
解得: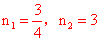 (不合题意舍去),∴
(不合题意舍去),∴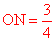 。
。
∴AM=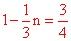 ,∴ M(
,∴ M( ,3),N(0,
,3),N(0, ) 。
) 。
把M( ,3),N(0,
,3),N(0, ), B(6,3)分别代入
), B(6,3)分别代入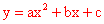 ,得
,得
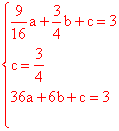 ,解得
,解得 。
。
∴抛物线的解析式为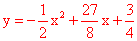 。
。
综上所述,抛物线的解析式为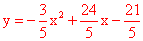 或
或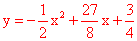 。
。
【考点】二次函数综合题,曲线上点的坐标与方程的关系,二次函数的性质,矩形的性质,锐角三角函数定义,勾股定理,解二元一次方程组。



科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)(0,2)(4,2),直线l的解析式为y = kx+5-4k(k > 0).

(1)当直线l经过点B时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点D;
(3)直线l与y轴交于点M,点N是线段DM上的一点, 且△NBD为等腰三角形,试探究:
①当函数y = kx+5-4k为正比例函数时,点N的个数有 个;
② 点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校为实施 国家“营养早餐”工程,食堂用甲、乙两种
国家“营养早餐”工程,食堂用甲、乙两种 原料配制成某种
原料配制成某种 营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
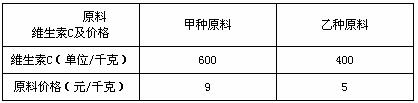
现要配制这种营养食品20千克,要求每千 克至少含有480单位的维生素C.设
克至少含有480单位的维生素C.设 购买甲种原料x千克.
购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
某山区的一种特产由于运输原因,长期只能在当地销售,当地政府对该特产的销售投资收益为:每投入x万元,可获得利润P=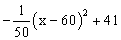 (万元)。当地政府拟规划加快开
(万元)。当地政府拟规划加快开 发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两
发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两 年中,每
年中,每 年都从100万元
年都从100万元 中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。
中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。 在外地销售的投资收益为:每投入
在外地销售的投资收益为:每投入 万元,可获利润Q=
万元,可获利润Q= (万元)。
(万元)。
(1)若不进行开发,求5年所获利润的最大值是多少?
 (2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数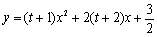
 , 在
, 在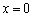
 和
和
 时的函数值相等.
时的函数值相等.
( 1)求二次函数的解析式;
1)求二次函数的解析式;
(2)若一次函数
 的图象与二次函数的图象都经过点
的图象与二次函数的图象都经过点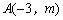
 ,求
,求
 和
和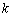
 的值;
的值;
(3) 设二次函数的图象与
设二次函数的图象与
 轴交于点
轴交于点
 (点
(点
 在点
在点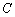
 的左侧),将二次函数的图象在点
的左侧),将二次函数的图象在点
 间的部分(含点
间的部分(含点
 和点
和点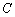
 )向左平移
)向左平移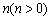
 个单位后得到的图象记为
个单位后得到的图象记为

 ,同时将(2)中得到的直线
,同时将(2)中得到的直线
 向右平移
向右平移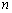
 个单位.请结合图象回答:当平移后的直线与图象
个单位.请结合图象回答:当平移后的直线与图象
 有公
有公 共点时,
共点时,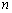
 的取值范围
的取值范围 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:y关于x的函数
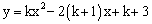 的图象与x轴有交点。
的图象与x轴有交点。
(1)求k的取值范围;
(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足 .
.
①求k的值;②当 时,请结合函数图象确定y的最大值和最小值。
时,请结合函数图象确定y的最大值和最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
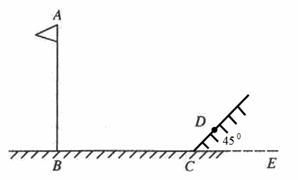
某校初三年级“数学兴趣小组”实地测量操场旗杆的高度.旗杆的影子落在操场和操场边的土坡上,如图所示,测得在操场上的影长BC=20 m,斜坡上的影长CD=2m,已知斜坡CD与操场平面的夹角为45°,同时测得身高l. 65m的学生在操场 上的影长为3.3 m.求旗杆AB的高度。(结果精确到1m)
65m的学生在操场 上的影长为3.3 m.求旗杆AB的高度。(结果精确到1m)
(提示:同一时刻物高与影长成正比.参考数据: ≈1.414.
≈1.414. ≈1.732.
≈1.732.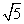 ≈2.236)
≈2.236)
查看答案和解析>>
科目:初中数学 来源: 题型:
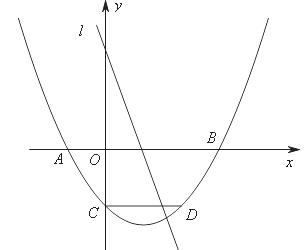
如图,抛物线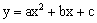 关于直线
关于直线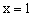 对称,与坐标轴交于A、B、C三点,且AB=4,点D
对称,与坐标轴交于A、B、C三点,且AB=4,点D 在抛物线上,直线
在抛物线上,直线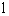 是一次函数
是一次函数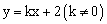 的图象,点O是坐标原点。
的图象,点O是坐标原点。
(1)求抛物线的解析式;
(2)把抛物线向左平移1个单位,再向上平移4个单位,所得抛物线与直线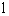 交于M、N两点,问在y轴负半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴
交于M、N两点,问在y轴负半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴 对称?若存在,求出P点坐标;若不存在,请说明理
对称?若存在,求出P点坐标;若不存在,请说明理 由.
由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com