
已知二次函数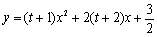
 , 在
, 在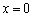
 和
和
 时的函数值相等.
时的函数值相等.
( 1)求二次函数的解析式;
1)求二次函数的解析式;
(2)若一次函数
 的图象与二次函数的图象都经过点
的图象与二次函数的图象都经过点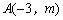
 ,求
,求
 和
和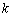
 的值;
的值;
(3) 设二次函数的图象与
设二次函数的图象与
 轴交于点
轴交于点
 (点
(点
 在点
在点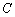
 的左侧),将二次函数的图象在点
的左侧),将二次函数的图象在点
 间的部分(含点
间的部分(含点
 和点
和点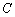
 )向左平移
)向左平移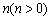
 个单位后得到的图象记为
个单位后得到的图象记为

 ,同时将(2)中得到的直线
,同时将(2)中得到的直线
 向右平移
向右平移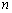
 个单位.请结合图象回答:当平移后的直线与图象
个单位.请结合图象回答:当平移后的直线与图象
 有公
有公 共点时,
共点时,
 的取值范围
的取值范围 .
.
解:(1)∵二次函数y=(t+1)x2+2(t+2)x+
在x=0和x=2时的函数值相等,
 ∴对称轴x=-=1
∴对称轴x=-=1
即-=1
解得,t=-
则二次函数的解析式为:y=(-+1)x2+2(-+2)x+-
即y=-(x+1)(x-3)或y=-(x-1)2+2,
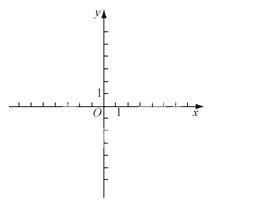
∴该函数图象的开口方向向下,且经过点(-1,0),(3,0),(0,),顶点坐标是(1,2).其图象如图所示: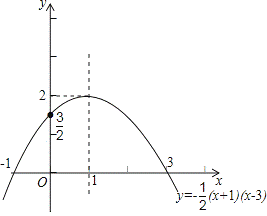
(2)∵二次函数的象经过点A(-3,m),
∴m=-(-3+1)(-3-3)=-6.
又∵一次函数y=kx+6的图象经过点A(-3,m),
∴m= -3k+6,即-6=-3k+6,
-3k+6,即-6=-3k+6,
解得,k=4.
综上所述,m和k的值分别是-6、4.
(3)解:由题意可知,点B、C间的部分图象的解析式是y=- x2+x+=--(x2-2x-3)=--(x-3)(x+1),-1≤x≤3,
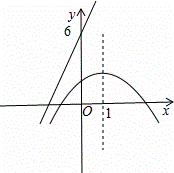


即n=0,
∵与已 知n>0相矛盾,
知n>0相矛盾,
∴平移后的直线与平移后的抛物线不相切,
∴结合图 象可知,如果平移后的直线与抛物线有公共点,
象可知,如果平移后的直线与抛物线有公共点,
则两个临界的交点为(-n-1,0),(3-n,0),
则0=4(-n -1)+6+n,
-1)+6+n,
n=,0=4 (3-n)+6+n,
(3-n)+6+n,
n=6,
即n的取值范围是:≤n≤6
【解析】


考点:用待定系 数法求二次函数解析式,二次函数的性质,二次函数图像上点的特点
数法求二次函数解析式,二次函数的性质,二次函数图像上点的特点
点评: 本题考查了待定系数法求二次函数的解析式,二次函数的
本题考查了待定系数法求二次函数的解析式,二次函数的 图象以及二次函数图象上点的坐标特
图象以及二次函数图象上点的坐标特 征.求得二次函数的解析式时,利用了二次函
征.求得二次函数的解析式时,利用了二次函 数图象的对称性质
数图象的对称性质


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合.三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,请直接写出 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,点A是双曲线y=
如图所示,点A是双曲线y=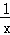 (x>0)上的一动点,过A作AC⊥y轴
(x>0)上的一动点,过A作AC⊥y轴 ,垂足为点C,作AC的垂直平分线双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,四边形ABCD的面积( )
,垂足为点C,作AC的垂直平分线双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,四边形ABCD的面积( )
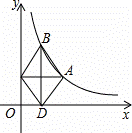
A.逐渐变小 B.由大变小再由小变大
C.由 小变大再有大变小 D.不变
小变大再有大变小 D.不变
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m) 与运行的水平距离x(m)满足关系式
与运行的水平距离x(m)满足关系式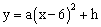 。已知球网与O点
。已知球网与O点 的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围);
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求 二次函数中二次项系数a的最大值。
二次函数中二次项系数a的最大值。

查看答案和解析>>
科目:初中数学 来源: 题型:
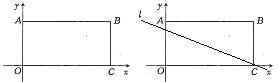
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线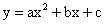
 过点B。
过点B。
(1)若a=-l,且抛物线与矩形有且只有三个交点B、D、E,求△ BDE的面积S的最大值;
(2)若抛物线与矩形有且只有三个交点B 、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指 针落在哪
针落在哪 一区域就可以获得相应的奖品.下表是活动进
一区域就可以获得相应的奖品.下表是活动进 行中的一组统计数据:
行中的一组统计数据:
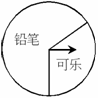

(1)计算并完成表格:


(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获得铅笔的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com