
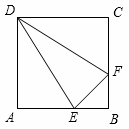
如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.若△DEF的面积为y,BF的长为x,则表示y与x的函数关系的图象大致是( )


A.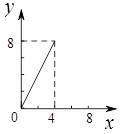

 B.
B.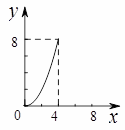

 C.
C.

 D.
D.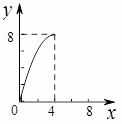


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
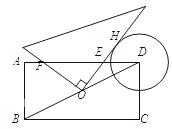
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合.三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,请直接写出 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
假期到了,学校组织19名女教师去外地培训,住宿时有2人间和3人间可供安排,若每个房间都要住满,共有几种安排方案( )
A.5种 B.4种 C.3种 D.2种
查看答案和解析>>
科目:初中数学 来源: 题型:
郑州市花卉种 植专业户王有才承包了30亩花圃,分别种植
植专业户王有才承包了30亩花圃,分别种植 康乃馨
康乃馨 和玫瑰花,有关成本、销售额见下表:
和玫瑰花,有关成本、销售额见下表:
| 种植种类 | 成本(万元/亩) | 销售额(万元/亩) |
| 康乃馨 | 2.4 | 3 |
| 玫瑰花 | 2 | 2.5 |
(1)2012年,王有才种植康乃馨20亩、 玫瑰花10亩,求王有才这一年共
玫瑰花10亩,求王有才这一年共 收益多少万元?(收益=销售额-成本)
收益多少万元?(收益=销售额-成本)
(2)2013年,王有才继续用这30亩花圃全部种植康乃馨和玫瑰花,计划投入成本不超过70万元.若每亩种植的成本 、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花
、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花 各多少亩?
各多少亩?
(3)已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg,根据(2)中的种植亩数,为了节约运输成本,实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍,结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两车从A地驶 向B地,
向B地, 甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
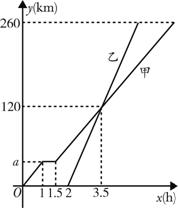

(1)求出图中a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函
 数表达式
数表达式 ,并写出相应
,并写出相应 的x的取值范围;
的x的取值范围;
(3)当甲车行驶多长时间时,两车恰好相距40km.
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,点A是双曲线y=
如图所示,点A是双曲线y=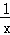 (x>0)上的一动点,过A作AC⊥y轴
(x>0)上的一动点,过A作AC⊥y轴 ,垂足为点C,作AC的垂直平分线双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,四边形ABCD的面积( )
,垂足为点C,作AC的垂直平分线双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,四边形ABCD的面积( )
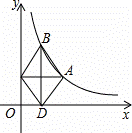
A.逐渐变小 B.由大变小再由小变大
C.由 小变大再有大变小 D.不变
小变大再有大变小 D.不变
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m) 与运行的水平距离x(m)满足关系式
与运行的水平距离x(m)满足关系式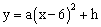 。已知球网与O点
。已知球网与O点 的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围);
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求 二次函数中二次项系数a的最大值。
二次函数中二次项系数a的最大值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com