
分析 (1)因为正比例函数y=kx的图象经过点(1,-3),所以-3=k,解之即可解决问题.
(2)设P(x,0),根据题意得出S△PAO=$\frac{1}{2}$×|x|•3=6,解方程即可.
解答 解:(1)∵正比例函数y=kx的图象经过A点(-2,3),
∴-2k=3,
∴k=-$\frac{3}{2}$
∴该正比例函数的解析式为:y=-$\frac{3}{2}$x.
(2)设P(x,0),
∴OP=|x|,
∵S△PAO=6,
∴$\frac{1}{2}$×|x|•3=6,
∴x1=4,x2=-4,
∴P(4,0)或P(-4,0).
点评 此题主要考查了待定系数法求正比例函数解析式,以及一次函数图象上点的坐标特征,三角形面积等,求得解析式上解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
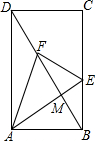 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{13}\sqrt{13}$ | D. | $\frac{2}{13}\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.
在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
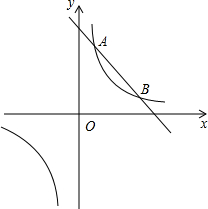 如图,反比例函数y1=$\frac{k}{x}$,(k>0)与一次函数y2=-x+5交于A(2,n)、B两点(A点在B点左边)
如图,反比例函数y1=$\frac{k}{x}$,(k>0)与一次函数y2=-x+5交于A(2,n)、B两点(A点在B点左边)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com