
【题目】如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=![]() (AB+AC).
(AB+AC).

【答案】(1)见详解;(2)见详解
【解析】
(1)根据线段垂直平分线求出BE=CE,根据角平分线性质求出EF=GE,即可Rt△BFE≌Rt△CGE;
(2)证明△AFE≌△AGE,推出AF=AG,即可得出答案.
证明:(1)连接BE和CE,
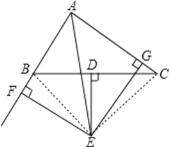
∵DE是BC的垂直平分线,
∴BE=CE,
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴∠BFE=∠EGC=90°,EF=EG,
在Rt△BFE和Rt△CGE中
![]()
∴Rt△BFE≌Rt△CGE(HL),
∴BF=CG;
(2)∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴∠AFE=∠AGE=90°,∠FAE=∠GAE,
在△AFE和△AGE中
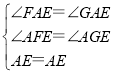
∴△AFE≌△AGE,
∴AF=AG,
∵BF=CG,
∴![]() (AB+AC)=
(AB+AC)=![]() (AF-BF+AG+CG)
(AF-BF+AG+CG)
=![]() (AF+AF)
(AF+AF)
=AF,
即AF=![]() (AB+AC).
(AB+AC).


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】工厂准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
![]() 求一只A型节能灯和一只B型节能灯的售价各是多少元?
求一只A型节能灯和一只B型节能灯的售价各是多少元?
![]() 工厂准备购进这两种型号的节能灯共50只,且A型节能灯的数量不多于B型节能灯数量的4倍,当购进A型节能灯m只时,工厂的总费用为w元.
工厂准备购进这两种型号的节能灯共50只,且A型节能灯的数量不多于B型节能灯数量的4倍,当购进A型节能灯m只时,工厂的总费用为w元.
![]() 写出
写出![]() 元
元![]() 与
与![]() 只
只![]() 之间的函数关系式,并写出自变量取值范围;
之间的函数关系式,并写出自变量取值范围;
![]() 如何购买A、B型节能灯,可以使总费用最少,且总费用最少是多少?
如何购买A、B型节能灯,可以使总费用最少,且总费用最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长均为1个单位的正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:

(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后得到的图形△A1B1C1;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC 中,∠BAC=90°,AB=AC=2,以 AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段 BD 的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文1张、数学2张、英语1张
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com