
 如图,抛物线y=
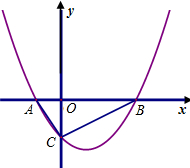
如图,抛物线y= x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.
x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上. x2-x+a其顶点在直线y=-2x上.
x2-x+a其顶点在直线y=-2x上. x2-x+a,
x2-x+a, (x2-2x)+a,
(x2-2x)+a, (x-1)2-
(x-1)2- +a,
+a, +a),
+a), +a=-2×1,
+a=-2×1, ;
; x2-x-
x2-x- ,
, x2-x-
x2-x- 与x轴交于点A,B,
与x轴交于点A,B, x2-x-
x2-x- ,
,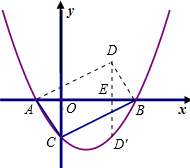
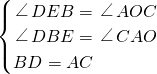
 x2-x-
x2-x- ,
, ),
), ,∴DE=
,∴DE= ,
, ),
), ),
), x2-x-
x2-x- ,
, ,右边=
,右边= ×4-2-
×4-2- =-
=- ,
,

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
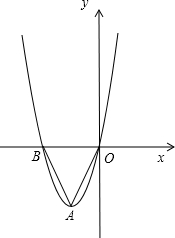 如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.
如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.查看答案和解析>>
科目:初中数学 来源: 题型:
 16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y
16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y查看答案和解析>>
科目:初中数学 来源: 题型:
 已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.
已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:
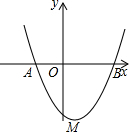 如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.
如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com