
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
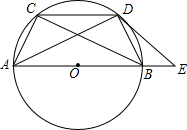 如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.
如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
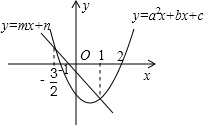 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )| A. | 1<x<2 | B. | x<-$\frac{3}{2}$或x>1 | C. | -$\frac{3}{2}$<x<2 | D. | -1<x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
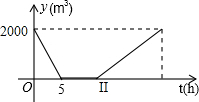 某游泳池内现存水2000m3,已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水-清洗-灌水”的过程,其中游泳池内剩余的水量ym3与换水时间th之间的函数关系如图所示.根据图象解答下列问题:
某游泳池内现存水2000m3,已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水-清洗-灌水”的过程,其中游泳池内剩余的水量ym3与换水时间th之间的函数关系如图所示.根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c>a>b | B. | a>c>b | C. | b>c>a | D. | a>b>c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com