
 ij��Ӿ�����ִ�ˮ2000m3����֪����Ӿ�ص���ˮ�ٶ��ǹ�ˮ�ٶȵ�2���������ڻ�ˮʱ��Ҫ��������ˮ-��ϴ-��ˮ���Ĺ��̣�������Ӿ����ʣ���ˮ��ym3�뻻ˮʱ��th֮��ĺ�����ϵ��ͼ��ʾ������ͼ�����������⣺
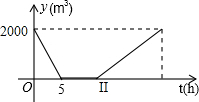
ij��Ӿ�����ִ�ˮ2000m3����֪����Ӿ�ص���ˮ�ٶ��ǹ�ˮ�ٶȵ�2���������ڻ�ˮʱ��Ҫ��������ˮ-��ϴ-��ˮ���Ĺ��̣�������Ӿ����ʣ���ˮ��ym3�뻻ˮʱ��th֮��ĺ�����ϵ��ͼ��ʾ������ͼ�����������⣺���� ��1����ͼ���֪������Ӿ��5��Сʱ��ˮ2000��m3���������ٶȹ�ʽ������ɣ������ˮ���ٶȺ�ʱ�伴�������ϴ����Ӿ�����õ�ʱ�䣻
��2�����ˮ�����е�y��m3���뻻ˮʱ��t��h��֮��ĺ�����ϵʽ��y=kt+b������11��0������21��1890������y=kt+b������ɣ�
��� �⣺��1������ͼ���֪������Ӿ��5��Сʱ��ˮ2000��m3����
�����Ӿ����ˮ���ٶ���2000��5=400��m3/h����
������ø���Ӿ�ع�ˮ���ٶ���400��0.5=200��m3/h����
�ɴ˵ù�ˮ2000m3��Ҫ��ʱ����2000��200=10��h����
����ϴ����Ӿ�����õ�ʱ����11-5=6��h����
��2�����ˮ�����е�y��m3���뻻ˮʱ��t��h��֮��ĺ�����ϵʽ��y=200t+b��
����11��0��������y=200t+b����b=-2200��
����ˮ�����е�y��m3����ʱ��t��h��֮��ĺ�����ϵʽ��y=200t-2200����11��t��21����
���� ���⿼����һ�κ�����Ӧ�ã���Ҫ����ѧ���ܷ��ʵ������ת������ѧ���⣬��Ŀ�Ƚϵ��ͣ���һ���ȽϺõ���Ŀ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
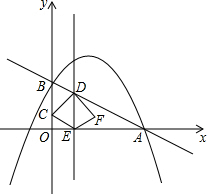 ��ͼ����ֱ֪��y=-$\frac{1}{2}$x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=-$\frac{1}{2}$x2+bx+c����A��B���㣮
��ͼ����ֱ֪��y=-$\frac{1}{2}$x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=-$\frac{1}{2}$x2+bx+c����A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{2}{3}$ | B�� | -5 | C�� | 0 | D�� | |-2| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com