
【题目】如果P 是正方形ABCD 内的一点,且满足∠APB+∠DPC=180°,那么称点P 是正方形 ABCD 的“对补点”.
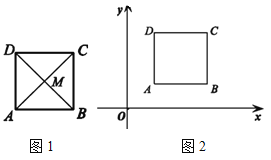
(1)如图1,正方形ABCD 的对角线AC,BD 交于点M,求证:点M 是正方形ABCD 的对补点;
(2)如图2,在平面直角坐标系中,正方形ABCD 的顶点A(1,1),C(3,3).除对角线交点外,请再写出一个该正方形的对补点的坐标,并证明.
【答案】(1)证明见解析;
(2)对补点如:N(![]() ,
, ![]() ).证明见解析
).证明见解析
【解析】试题分析:(1)根据正方形的对角线互相垂直,得到∠DMC=∠AMB=90°,从而得到点M是正方形ABCD的对补点.(2) 在直线y=x(1<x<3)或直线y=-x+4(1<x<3)上
除(2,2)外的任意点均可,通过证明△DCN≌△BCN,得到∠CND=∠CNB,利用邻补角的性质即可得出结论.
试题解析:
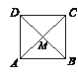
(1)
∵四边形ABCD是正方形,
∴ AC⊥BD.
∴ ∠DMC=∠AMB=90°.
即 ∠DMC+∠AMB=180°.
∴ 点M是正方形ABCD的对补点.
(2)对补点如:N(![]() ,
, ![]() ).
).
说明:在直线y=x(1<x<3)或直线y=-x+4(1<x<3)上
除(2,2)外的任意点均可.
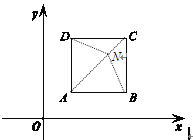
证明(方法一):
连接AC ,BD
由(1)得此时对角线的交点为(2,2).
设直线AC的解析式为:y=kx+b,
把点A(1,1),C(3,3)分别代入,
可求得直线AC的解析式为:y=x.
则点N(![]() ,
, ![]() )是直线AC上除对角线交点外的一点,且在正方形ABCD内.
)是直线AC上除对角线交点外的一点,且在正方形ABCD内.
连接AC,DN,BN,
∵ 四边形ABCD是正方形,
∴ DC=BC,∠DCN=∠BCN.
又∵ CN=CN,
∴ △DCN≌△BCN.
∴ ∠CND=∠CNB.
∵ ∠CNB+∠ANB=180°,
∴ ∠CND+∠ANB=180°.
∴ 点N是正方形ABCD的对补点.
证明(方法二):
连接AC ,BD,
由(1)得此时对角线的交点为(2,2).
设点N是线段AC上的一点(端点A,C及对角线交点除外),
连接AC,DN,BN,
∵ 四边形ABCD是正方形,
∴ DC=BC,∠DCN=∠BCN.
又∵ CN=CN,
∴ △DCN≌△BCN.
∴ ∠CND=∠CNB.
∵ ∠CNB+∠ANB=180°,
∴ ∠CND+∠ANB=180°.
∴ 点N是正方形ABCD除对角线交点外的补点.
设直线AC的解析式为:y=kx+b,
把点A(1,1),C(3,3)分别代入,可求得直线AC的解析式为:y=x.
在1<x<3范围内,任取一点均为该正方形的对补点,如N(![]() ,
, ![]() ).
).


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的个数有( )
①射线AB与射线BA表示同一条射线.
②若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3.
③一条射线把一个角分成两个角,这条射线叫这个角的平分线.
④连结两点的线段叫做两点之间的距离.
⑤40°50ˊ=40.5°.
⑥互余且相等的两个角都是45°.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为( ) 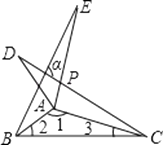
A.80°
B.100°
C.60°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽像出的几何图形,B,C,E在同一条直线上,连结DC. 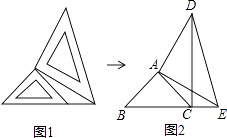
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的宇母);
(2)证明:DC⊥BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com