Question

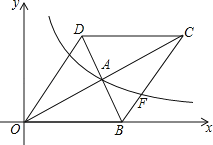
【题目】如图，在平面直角坐标系中，菱形OBCD的边OB在x轴正半轴上，反比例函数y=（x＞0）的图象经过该菱形对角线的交点A，且与边BC交于点F．若点D的坐标为（6，8），则点F的坐标是 ．

Answer 1

【答案】（12，）．

【解析】

试题分析：首先过点D作DM⊥x轴于点M，过点F作FE⊥x于点E，由点D的坐标为（6，8），可求得菱形OBCD的边长，又由点A是BD的中点，求得点A的坐标，利用待定系数法即可求得反比例函数y=（x＞0）的解析式，然后由tan∠FBE=tan∠DOM===，可设EF=4a，BE=3a，则点F的坐标为：（10+3a，4a），即可得方程4a（10+3a）=32，继而求得a的值，则可求得答案．

解：过点D作DM⊥x轴于点M，过点F作FE⊥x于点E，

∵点D的坐标为（6，8），

∴OD==10，

∵四边形OBCD是菱形，

∴OB=OD=10，

∴点B的坐标为：（10，0），

∵AB=AD，即A是BD的中点，

∴点A的坐标为：（8，4），

∵点A在反比例函数y=上，

∴k=xy=8×4=32，

∵OD∥BC，

∴∠DOM=∠FBE，

∴tan∠FBE=tan∠DOM===，

设EF=4a，BE=3a，

则点F的坐标为：（10+3a，4a），

∵点F在反比例函数y=上，

∴4a（10+3a）=32，

即3a2+10a﹣8=0，

解得：a1=，a2=﹣4（舍去），

∴点F的坐标为：（12，）．

故答案为：（12，）．