
���� ��1���ٽ��������Ķ��壬�������ݣ����Ԫһ�η����鼴�ɵó����ۣ�
�ڽ�a��b��ֵ����ԭ����ʽ�У���m��ʾ��M���ɶ��κ��������ʼ����ҳ�M��ȡֵ��Χ���Ӷ��ó�k��ֵ��
��2��x[]y=y[]x�ó�����a��b��x��y�ĵ�ʽ���ɶ�����ʵ��x��y���������ҳ���Ϊ0�Ĵ���ʽa+4b=0���Ӷ��ó����ۣ�
��� �⣺��1������1[]2=3��-1[]3=-2����
$\left\{\begin{array}{l}{a-4b=12}\\{-a-6b=-2}\end{array}\right.$�����$\left\{\begin{array}{l}{a=8}\\{b=-1}\end{array}\right.$��
��a��ֵΪ8��b��ֵΪ-1��
�ڰ�a=8��b=-1����x[]y=$\frac{ax-2by}{2x+y}$����x[]y=$\frac{8x+2y}{2x+y}$��
M=��m2-m-1��[]��2m-2m2��=-2m2+2m+4=-2${��m-\frac{1}{2}��}^{2}$+$\frac{9}{2}$��
�֡�-1��m��3��
�൱m=$\frac{1}{2}$ʱ��Mȡ���ֵ$\frac{9}{2}$��
��m=-1ʱ��M=0��
��m=3ʱ��M=-8��
��-8��M��$\frac{9}{2}$=4$\frac{1}{2}$��
��k=8+4+1=13��
��2����x[]y=y[]x��
��$\frac{ax-2by}{2x+y}$=$\frac{ay-2bx}{2y+x}$��
��ay2-ax2+4by2-4bx2=0��
��a��y2-x2��+4b��y2-x2��=0��
����a+4b����y2-x2��=0��
�߶�����ʵ��x��y��������
��a+4b=0��
��a=-4b��
���� ���⿼���˽��Ԫһ�η������Լ����κ��������ʣ�����Ĺؼ�����1���ٴ������ݽ��Ԫһ�η����飻�ڽ�϶��κ���������Ѱ����ֵ����2�����붨��ʽ��Ѱ�Һ�Ϊ0���������������е��⣬�ѶȲ����������漰���µ����������ѧ����������⣬��ʵ�ڽ���¶������͵���Ŀʱ�����㶼�Ǻܼģ�ֻҪ�μ�����Ĺ���������������Ӽ��ɵó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��A�ǡ�O��һ�㣬ֱ��MN����A����B��MN�ϵ���һ�㣬��C��OB���е㣬AC=$\frac{1}{2}$OB������P�ǡ�O�ϵ�һ�����㣬�ҡ�OBA=30�㣬AB=$2\sqrt{3}$ʱ�����APC����������ֵ��
��ͼ����֪��A�ǡ�O��һ�㣬ֱ��MN����A����B��MN�ϵ���һ�㣬��C��OB���е㣬AC=$\frac{1}{2}$OB������P�ǡ�O�ϵ�һ�����㣬�ҡ�OBA=30�㣬AB=$2\sqrt{3}$ʱ�����APC����������ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
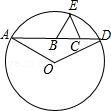 ��ͼ��A��B��C��D����Ϊһֱ����4���㣬BC=4����BCEΪ�ȱ������Σ���O��A��D��E���㣬�ҡ�AOD=120�㣮��AB=x��CD=y����y��x�ĺ�����ϵʽΪy=$\frac{16}{x}$��
��ͼ��A��B��C��D����Ϊһֱ����4���㣬BC=4����BCEΪ�ȱ������Σ���O��A��D��E���㣬�ҡ�AOD=120�㣮��AB=x��CD=y����y��x�ĺ�����ϵʽΪy=$\frac{16}{x}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4029x | B�� | 4029x2 | C�� | 4027x | D�� | 4027x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
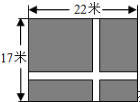 ��ͼ����һ�鳤Ϊ22m����Ϊ17m�ľ��ε����ڣ�Ҫ��������ͬ�����һ��ഹֱ�ĵ�·��������·�ֱ�����ε�һ����ƽ�У������µ����ϲ�ƺ��Ҫʹ��ƺ������ﵽ300m2�����·�Ŀ�Ϊx m�����������з��̣�20-x����32-x��=300��
��ͼ����һ�鳤Ϊ22m����Ϊ17m�ľ��ε����ڣ�Ҫ��������ͬ�����һ��ഹֱ�ĵ�·��������·�ֱ�����ε�һ����ƽ�У������µ����ϲ�ƺ��Ҫʹ��ƺ������ﵽ300m2�����·�Ŀ�Ϊx m�����������з��̣�20-x����32-x��=300���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��-2 | B�� | -3��2 | C�� | 3��2 | D�� | -3��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��1 | B�� | k��$\frac{1}{3}$ | C�� | $\frac{1}{3}$��k��1 | D�� | k��$\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com